OSKR/OKAI: Systematic Optimization of Key Encapsulation Mechanisms from Module Lattice

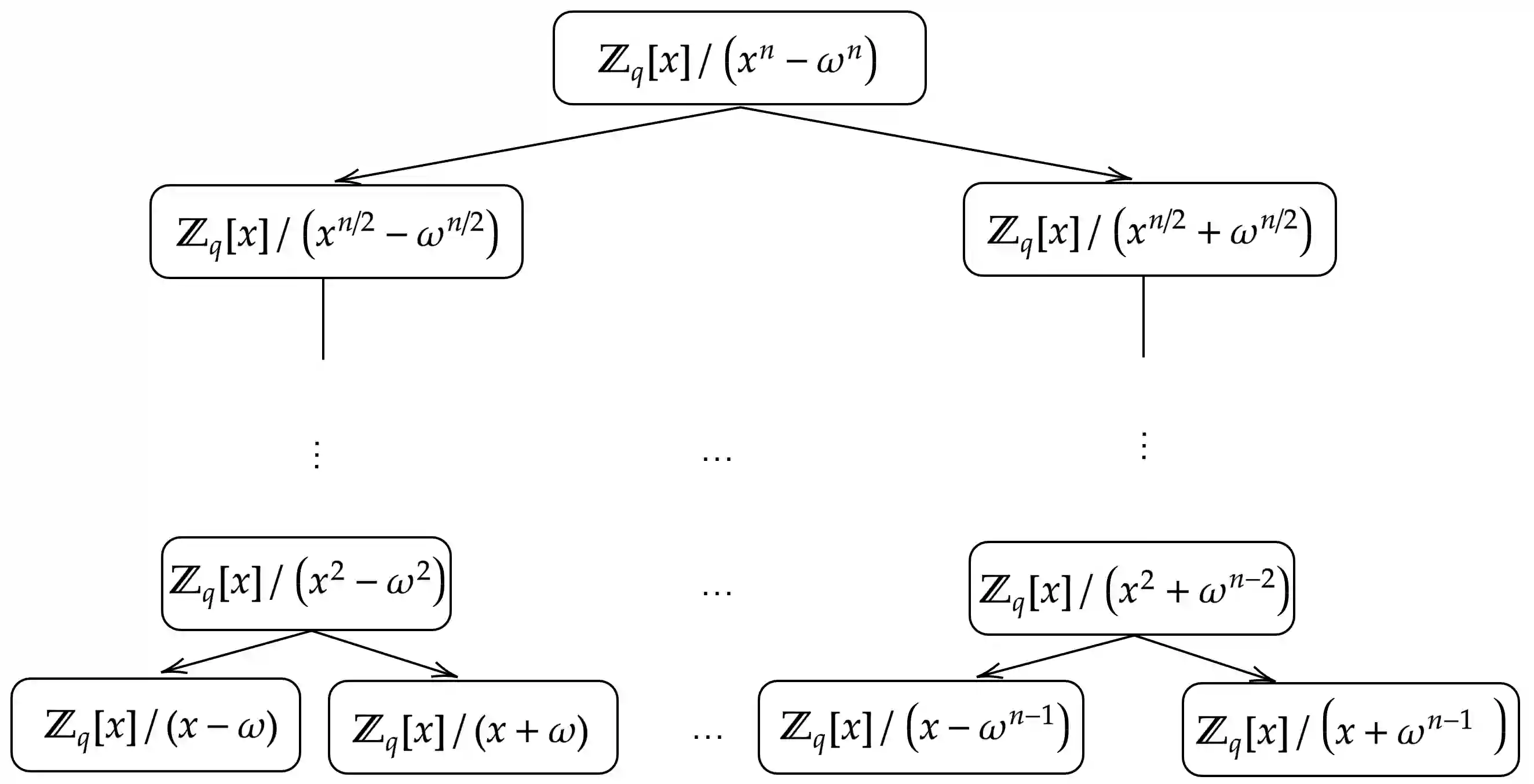
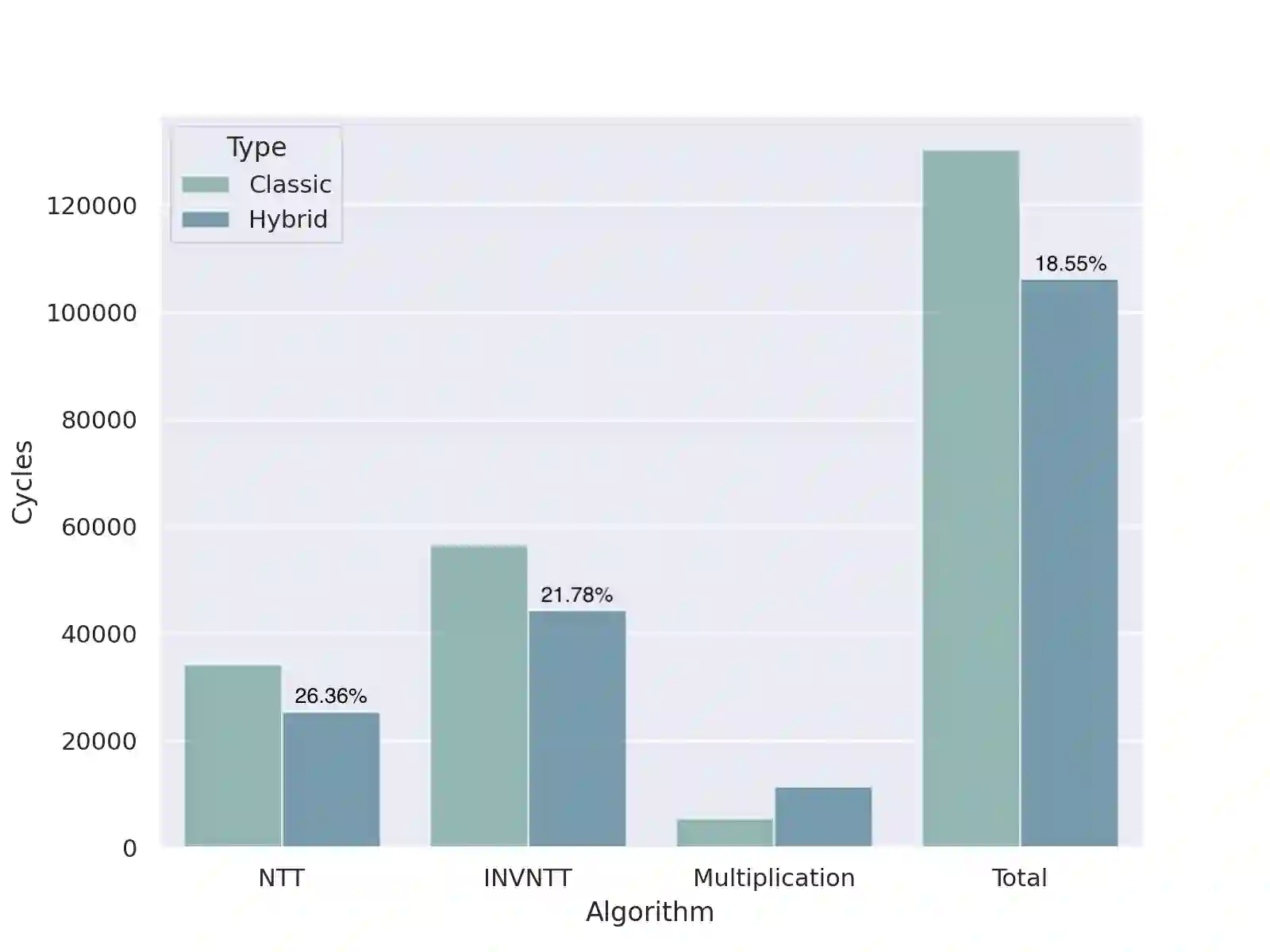
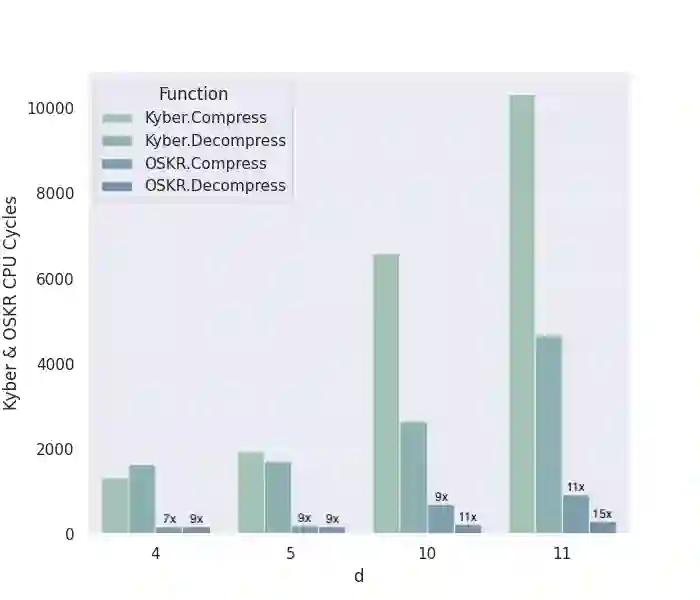
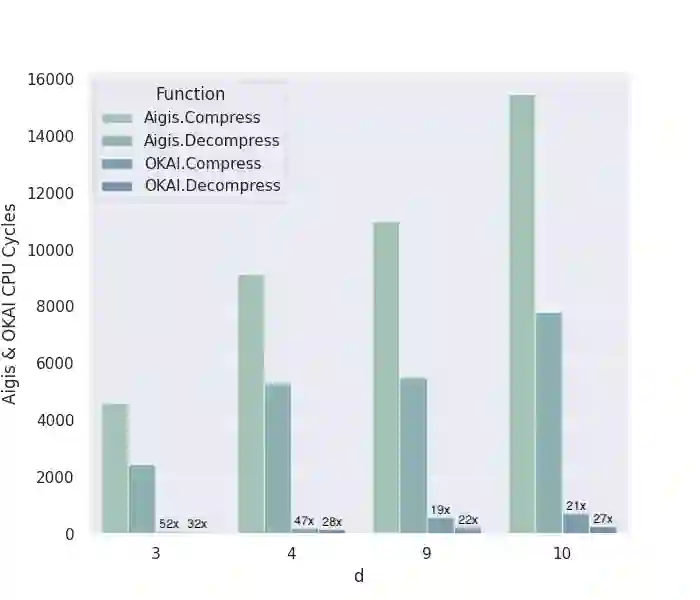
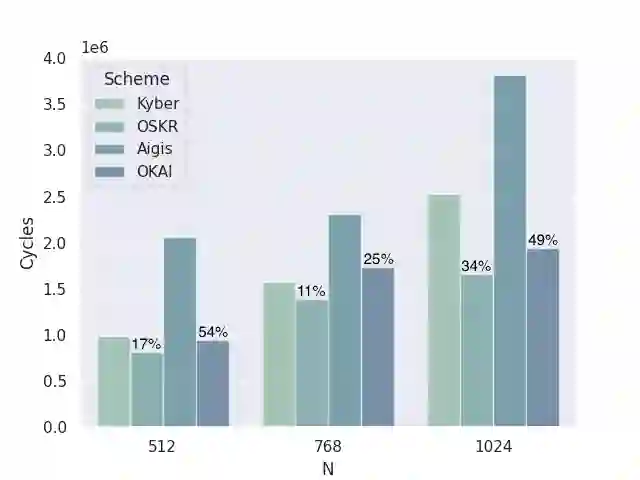
In this work, we make \emph{systematic} optimizations of key encapsulation mechanisms (KEM) based on module learning-with-errors (MLWE), covering algorithmic design, fundamental operation of number-theoretic transform (NTT), approaches to expanding encapsulated key size, and optimized implementation coding. We focus on Kyber (now in the Round-3 finalist of NIST PQC standardization) and Aigis (a variant of Kyber proposed at PKC 2020). By careful analysis, we first observe that the algorithmic design of Kyber and Aigis can be optimized by the mechanism of asymmetric key consensus with noise (AKCN) proposed in \cite{JZ16,JZ19}. Specifically, the decryption process can be simplified with AKCN, leading to a both faster and less error-prone decryption process. Moreover, the AKCN-based optimized version has perfect compatibility with the deployment of Kyber/Aigis in reality, as they can run on the same parameters, the same public key, and the same encryption process. We make a systematic study of the variants of NTT proposed in recent years for extending its applicability scope, make concrete analysis of their exact computational complexity, and in particular show their equivalence. We then present a new variant named hybrid-NTT (H-NTT), combining the advantages of existing NTT methods, and derive its optimality in computational complexity. The H-NTT technique not only has larger applicability scope but also allows for modular and unified implementation codes of NTT operations even with varying module dimensions. We analyze and compare the different approaches to expand the size of key to be encapsulated (specifically, 512-bit key for dimension of 1024), and conclude with the most economic approach. To mitigate the compatibility issue in implementations we adopt the proposed H-NTT method.