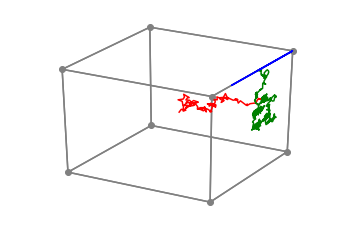
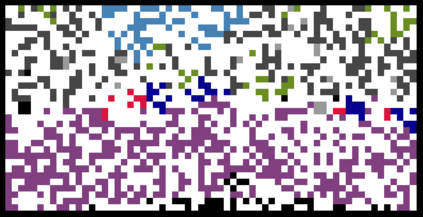
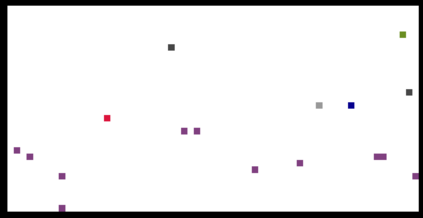
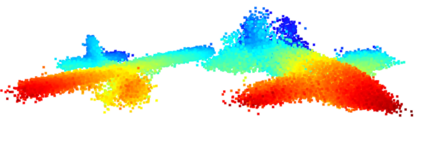
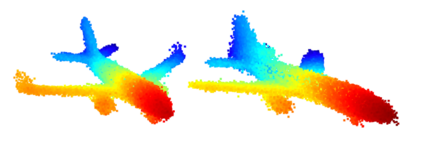
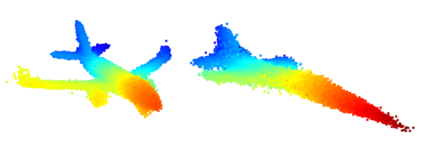
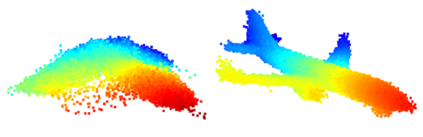
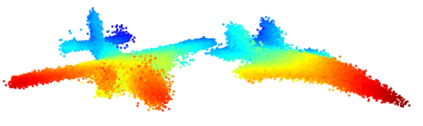
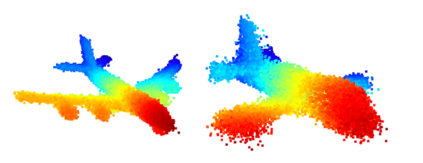
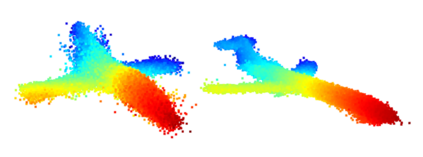
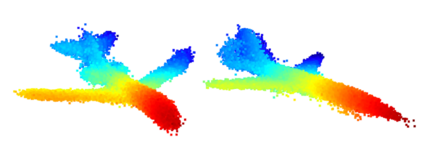
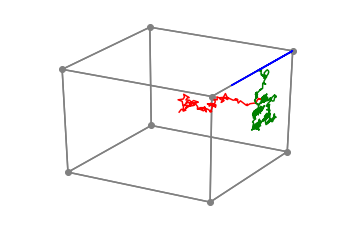
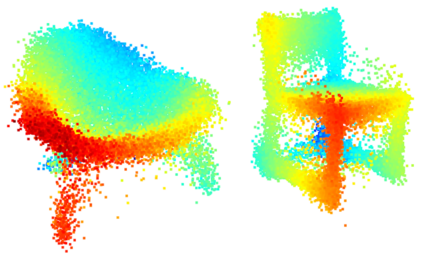We propose a family of First Hitting Diffusion Models (FHDM), deep generative models that generate data with a diffusion process that terminates at a random first hitting time. This yields an extension of the standard fixed-time diffusion models that terminate at a pre-specified deterministic time. Although standard diffusion models are designed for continuous unconstrained data, FHDM is naturally designed to learn distributions on continuous as well as a range of discrete and structure domains. Moreover, FHDM enables instance-dependent terminate time and accelerates the diffusion process to sample higher quality data with fewer diffusion steps. Technically, we train FHDM by maximum likelihood estimation on diffusion trajectories augmented from observed data with conditional first hitting processes (i.e., bridge) derived based on Doob's $h$-transform, deviating from the commonly used time-reversal mechanism. We apply FHDM to generate data in various domains such as point cloud (general continuous distribution), climate and geographical events on earth (continuous distribution on the sphere), unweighted graphs (distribution of binary matrices), and segmentation maps of 2D images (high-dimensional categorical distribution). We observe considerable improvement compared with the state-of-the-art approaches in both quality and speed.
翻译:我们建议了一个“第一击发射模型”(FHDM)系列,这是产生数据的数据的深重基因模型,其传播过程在随机的第一击时即终止。这产生标准的固定时间扩散模型的延伸,该模型在预先确定的时间即终止。虽然标准的传播模型是为连续的、不受限制的数据设计的,但FHDM自然设计来学习连续和一系列离散和结构域的分布。此外,FHDM允许根据实例的终止时间,加速传播过程,以较少的传播步骤抽样提供质量更高的数据。技术上,我们对FHDM进行了培训,对根据以Doob's $h$-transform为基础的有条件的第一次打击过程(即桥梁)所观察到的数据所强化的传播路径进行最大可能性估计。虽然标准的传播模型是用于连续和一系列离散时间和结构域。我们应用FHDMM在诸如点云(一般持续分布)、气候和地球的地理事件(持续地块分布不重)、不加权的图表(硬度矩阵矩阵的分布)以及2D级图像的分层分布图(我们观测的高度)。
相关内容
Source: Apple - iOS 8