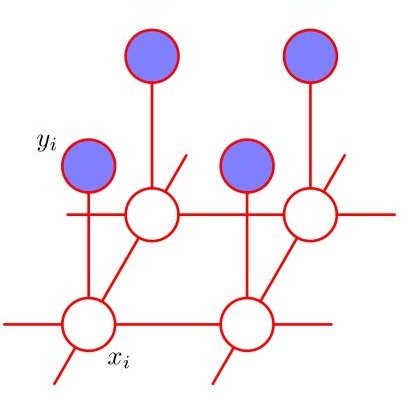
Discrete undirected graphical models, also known as Markov Random Fields (MRFs), can flexibly encode probabilistic interactions of multiple variables, and have enjoyed successful applications to a wide range of problems. However, a well-known yet little studied limitation of discrete MRFs is that they cannot capture context-specific independence (CSI). Existing methods require carefully developed theories and purpose-built inference methods, which limit their applications to only small-scale problems. In this paper, we propose the Markov Attention Model (MAM), a family of discrete MRFs that incorporates an attention mechanism. The attention mechanism allows variables to dynamically attend to some other variables while ignoring the rest, and enables capturing of CSIs in MRFs. A MAM is formulated as an MRF, allowing it to benefit from the rich set of existing MRF inference methods and scale to large models and datasets. To demonstrate MAM's capabilities to capture CSIs at scale, we apply MAMs to capture an important type of CSI that is present in a symbolic approach to recurrent computations in perceptual grouping. Experiments on two recently proposed synthetic perceptual grouping tasks and on realistic images demonstrate the advantages of MAMs in sample-efficiency, interpretability and generalizability when compared with strong recurrent neural network baselines, and validate MAM's capabilities to efficiently capture CSIs at scale.
翻译:在本文中,我们提出了Markov 注意模型(MAM),这是一个包含关注机制的离散管理成果框架的组合。关注机制允许变量动态地处理某些其他变量而忽略其余变量,并使得能够在管理成果框架中捕捉到 CSI。一个已知但很少研究的限制是,离散管理成果框架的局限性是,它们无法捕捉特定背景的独立性(CSI)。现有方法要求精心开发的理论和目的设定的推断方法,这些理论和目的设定的推断方法将其应用仅限于小规模问题。在本文中,我们提出了Markov 注意模型(MAM),这是一个包含关注机制的离散管理成果框架的组合。关注机制允许变量动态地处理其他一些变量,同时忽略其余变量,并使得能够在管理成果框架中捕捉到 CSI 。一个MAM 被设计成一个管理成果框架,使其能够从丰富的现有MRF误算方法和规模扩大到大型模型和数据集。为了展示MAM在规模上获取大量CIMIS的能力,我们运用了一种重要的CIMS,这是在现实性图像的反复计算方法中反复计算方法,同时展示了MIS的精准性基准,最近提出的CMASI在模拟模型上展示了两个组合的精准的精准性模型的精准性模型。