On Variance Estimation of Random Forests

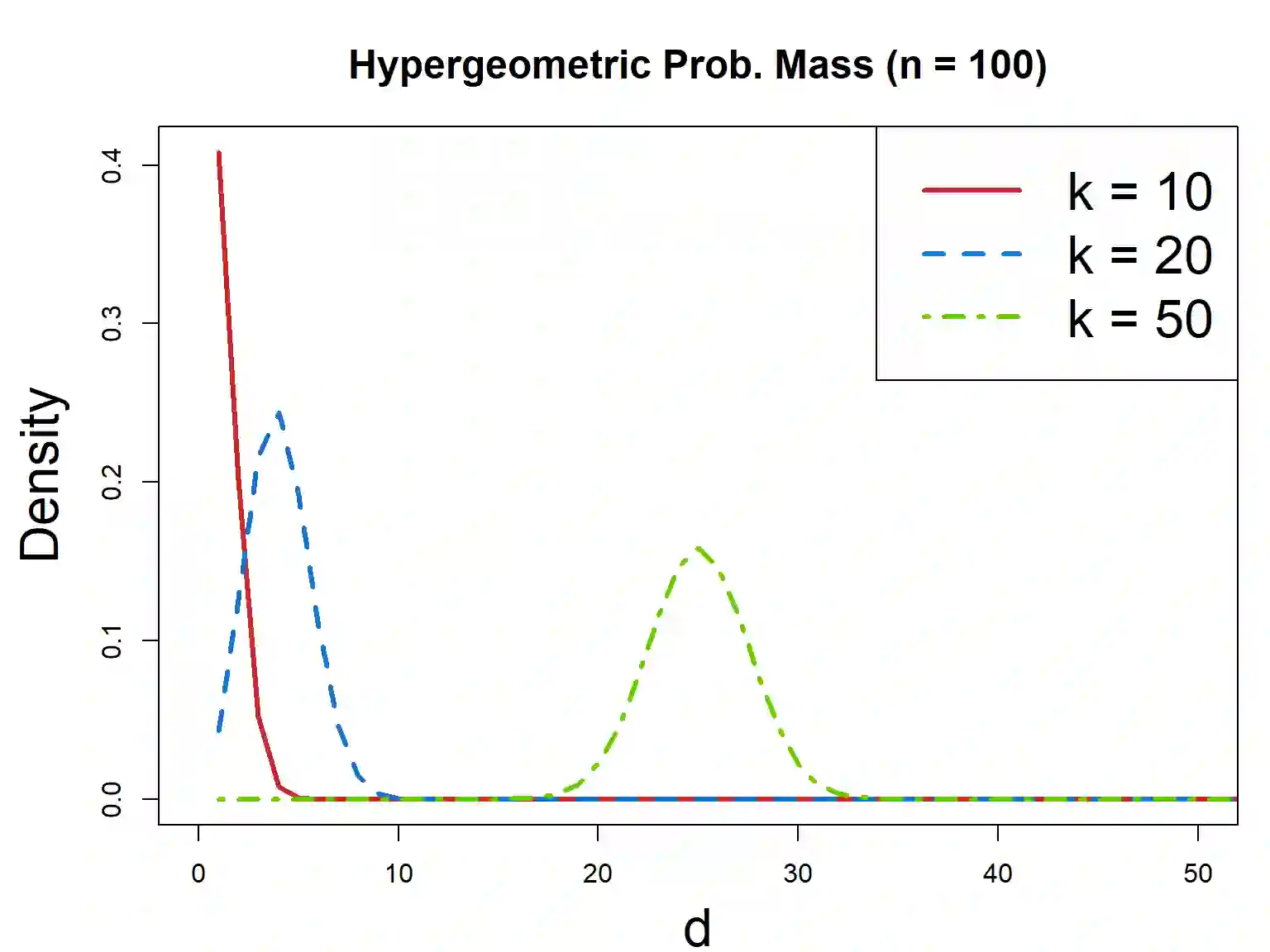
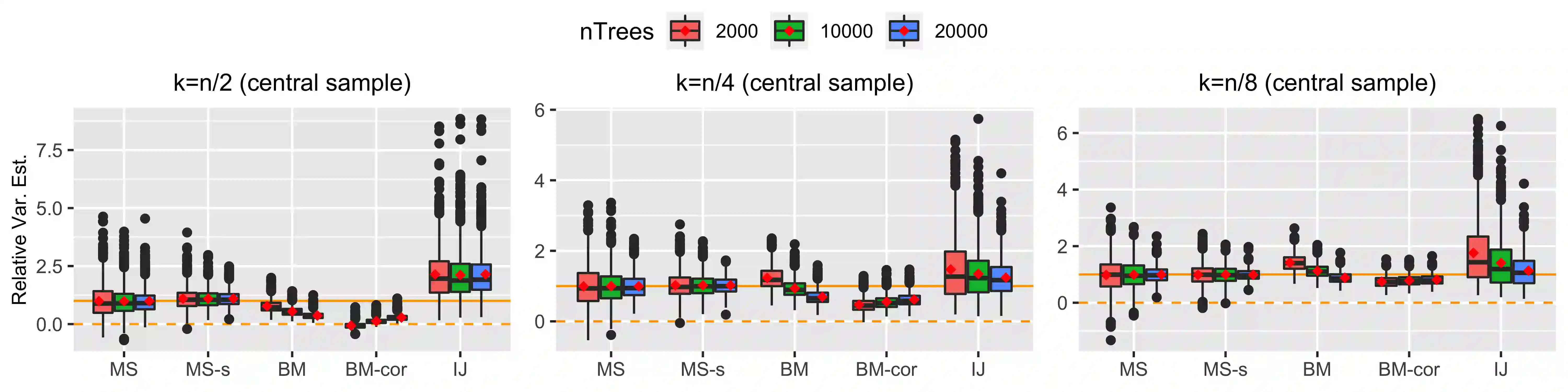
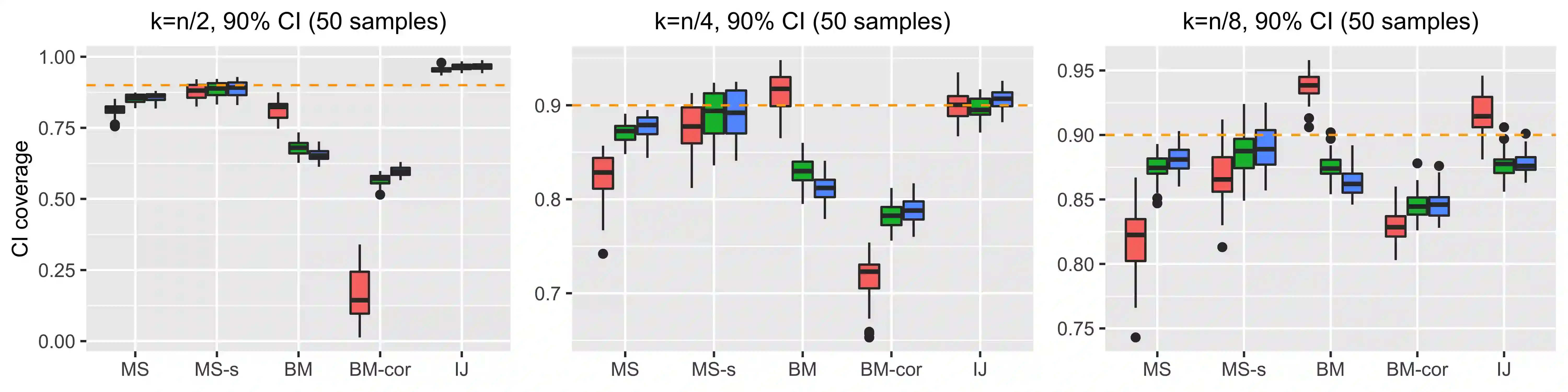
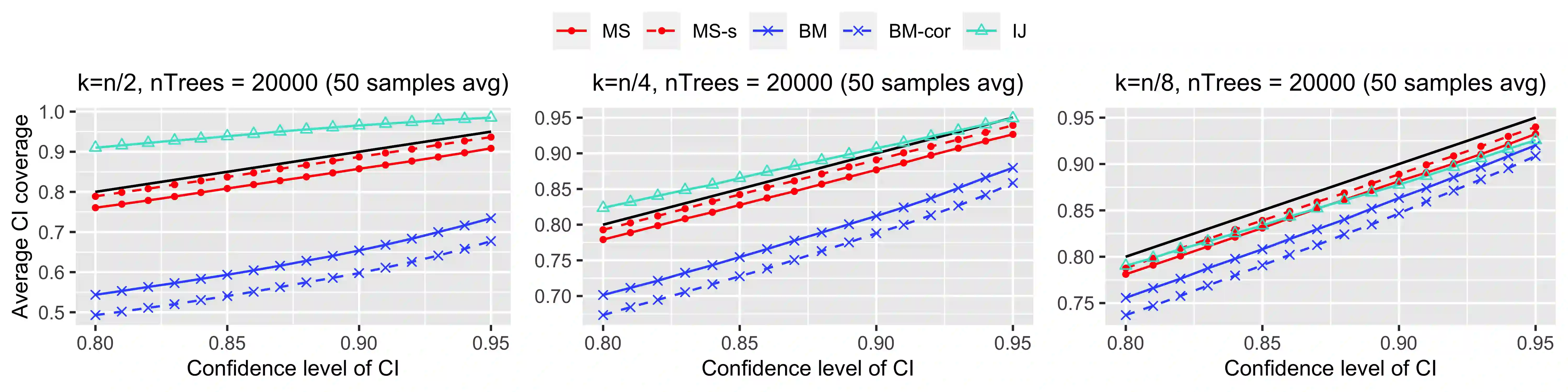
Ensemble methods based on subsampling, such as random forests, are popular in applications due to their high predictive accuracy. Existing literature views a random forest prediction as an infinite-order incomplete U-statistic to quantify its uncertainty. However, these methods focus on a small subsampling size of each tree, which is theoretically valid but practically limited. This paper develops an unbiased variance estimator based on incomplete U-statistics, which allows the tree size to be comparable with the overall sample size, making statistical inference possible in a broader range of real applications. Simulation results demonstrate that our estimators enjoy lower bias and more accurate confidence interval coverage without additional computational costs. We also propose a local smoothing procedure to reduce the variation of our estimator, which shows improved numerical performance when the number of trees is relatively small. Further, we investigate the ratio consistency of our proposed variance estimator under specific scenarios. In particular, we develop a new "double U-statistic" formulation to analyze the Hoeffding decomposition of the estimator's variance.