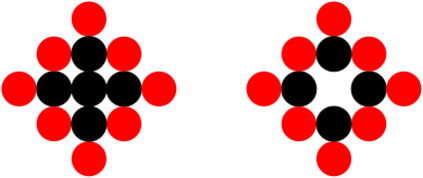
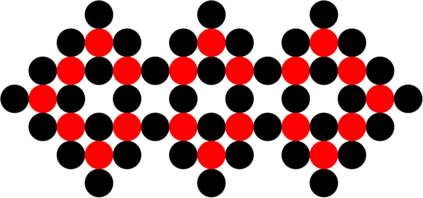
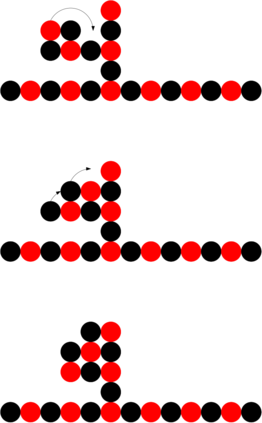
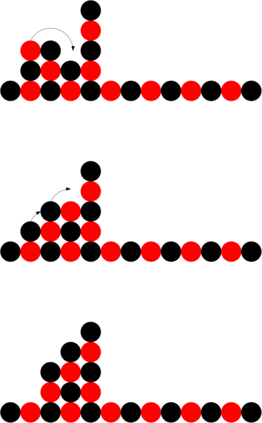
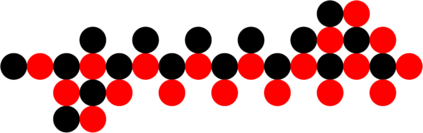
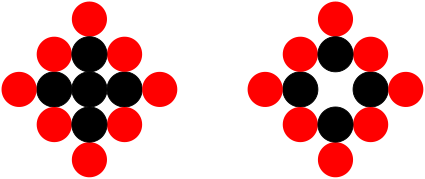
We study a model of programmable matter systems consisting of $n$ devices lying on a 2-dimensional square grid which are able to perform the minimal mechanical operation of rotating around each other. The goal is to transform an initial shape A into a target shape B. We investigate the class of shapes which can be constructed in such a scenario under the additional constraint of maintaining global connectivity at all times. We focus on the scenario of transforming nice shapes, a class of shapes consisting of a central line $L$ where for all nodes $u$ in $S$ either $u \in L$ or $u$ is connected to $L$ by a line of nodes perpendicular to $L$. We prove that by introducing a minimal 3-node seed it is possible for the canonical shape of a line of $n$ nodes to be transformed into a nice shape of $n-1$ nodes. We use this to show that a 4-node seed enables the transformation of nice shapes of size $n$ into any other nice shape of size $n$ in $O(n^2)$ time. We leave as an open problem the expansion of the class of shapes which can be constructed using such a seed to include those derived from nice shapes.
翻译:我们研究一个可编程物质系统模型,该模型由位于二维方格上的、能够进行最小机械旋转操作的二维平方格上的零美元装置组成。目标是将最初的形状A转化为目标形状B。我们调查在这种情景下,在保持全球连通性的额外制约下,可以在这种情景下建造的形状类别。我们重点研究改变优美形状的设想,这种形状类别由中央线构成,由一列美元构成,即中央线构成,对于所有节点而言,以美元或以美元计算,或以美元计算,或以美元计算,或以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算。美元计算,以美元计算。美元计算。美元计算,以美元计算。美元计算,以美元计算,以美元计算,以美元计算,以美元计算。美元计算。美元计算。美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,计算,计算,计算,计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算。美元计算。美元计算。美元计算。美元计算。美元计算。美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,以美元计算,