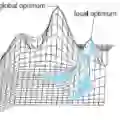
$k$-means clustering is a fundamental problem in various disciplines. This problem is nonconvex, and standard algorithms are only guaranteed to find a local optimum. Leveraging the structure of local solutions characterized in [1], we propose a general algorithmic framework for escaping undesirable local solutions and recovering the global solution (or the ground truth). This framework consists of alternating between the following two steps iteratively: (i) detect mis-specified clusters in a local solution and (ii) improve the current local solution by non-local operations. We discuss implementation of these steps, and elucidate how the proposed framework unifies variants of $k$-means algorithm in literature from a geometric perspective. In addition, we introduce two natural extensions of the proposed framework, where the initial number of clusters is misspecified. We provide theoretical justification for our approach, which is corroborated with extensive experiments.
翻译:以美元计价的集群是不同学科中的一个基本问题。 这个问题是非混凝土的问题,标准算法只能保证找到一个当地最佳的。 利用[1]中当地解决办法的结构,我们提议一个一般性的算法框架,以逃避不可取的地方解决办法和恢复全球解决办法(或地面真相),这一框架包括以下两个步骤的迭代交替:(一) 在当地解决办法中发现错定的集群,和(二) 通过非当地行动改进目前的本地解决办法。我们讨论这些步骤的执行情况,并阐明拟议框架如何从几何角度统一文学中以美元计价算法的变量。此外,我们引入了拟议框架的两个自然扩展,其中最初的集群数目被错误地描述。我们为我们的方法提供了理论上的理由,并得到了广泛的实验的证实。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem