Quantifying Ignorance in Individual-Level Causal-Effect Estimates under Hidden Confounding

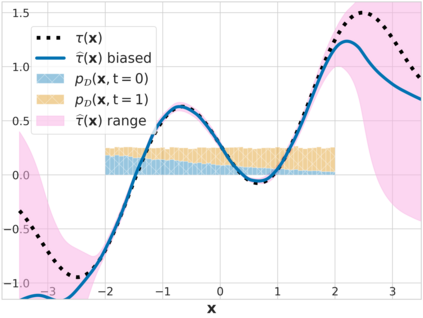
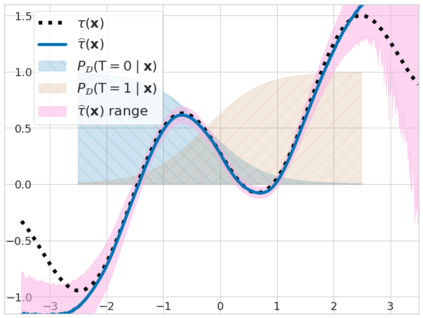
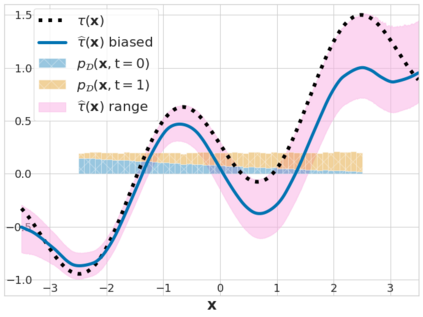
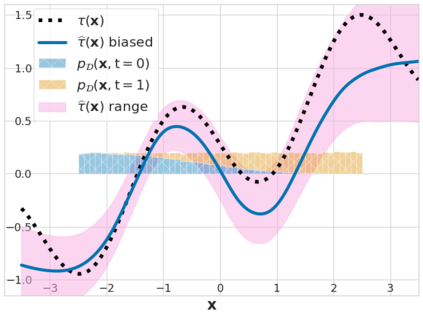
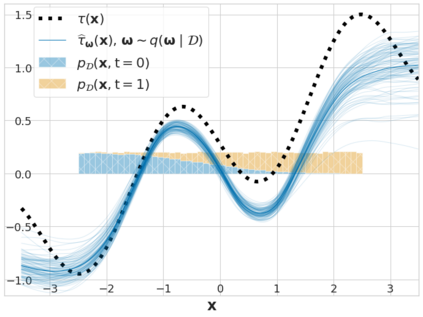
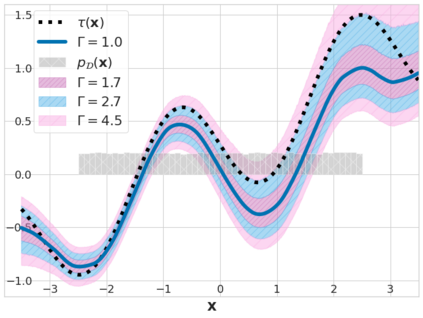
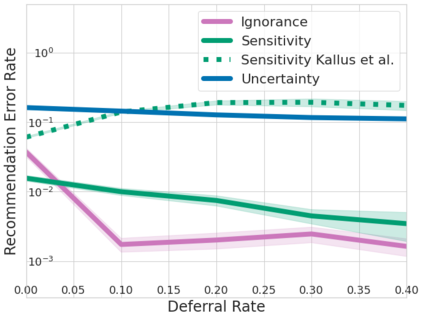
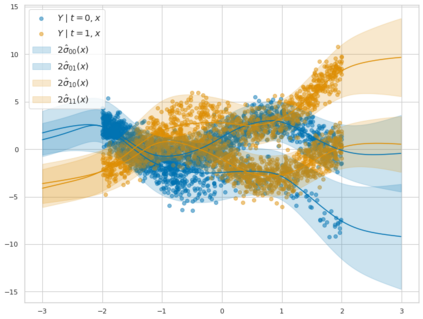
We study the problem of learning conditional average treatment effects (CATE) from high-dimensional, observational data with unobserved confounders. Unobserved confounders introduce ignorance -- a level of unidentifiability -- about an individual's response to treatment by inducing bias in CATE estimates. We present a new parametric interval estimator suited for high-dimensional data, that estimates a range of possible CATE values when given a predefined bound on the level of hidden confounding. Further, previous interval estimators do not account for ignorance about the CATE stemming from samples that may be underrepresented in the original study, or samples that violate the overlap assumption. Our novel interval estimator also incorporates model uncertainty so that practitioners can be made aware of out-of-distribution data. We prove that our estimator converges to tight bounds on CATE when there may be unobserved confounding, and assess it using semi-synthetic, high-dimensional datasets.