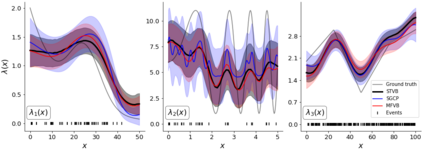
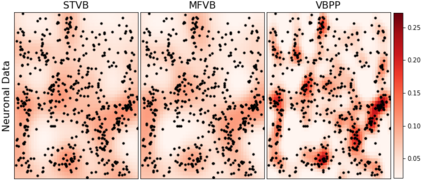
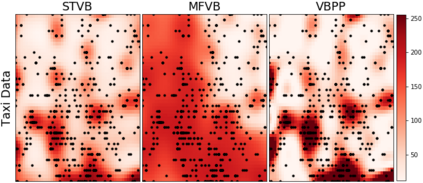
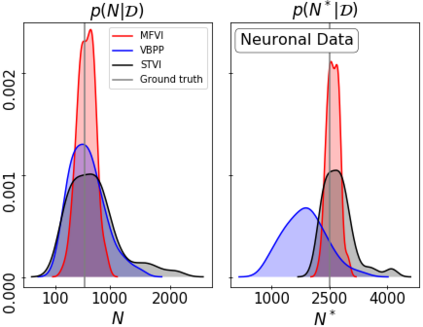
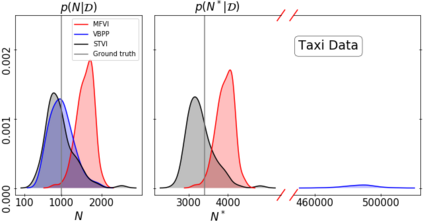
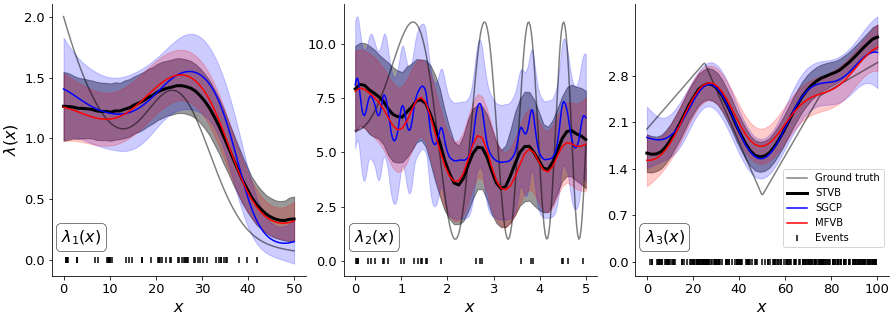
We propose a scalable framework for inference in an inhomogeneous Poisson process modeled by a continuous sigmoidal Cox process that assumes the corresponding intensity function is given by a Gaussian process (GP) prior transformed with a scaled logistic sigmoid function. We present a tractable representation of the likelihood through augmentation with a superposition of Poisson processes. This view enables a structured variational approximation capturing dependencies across variables in the model. Our framework avoids discretization of the domain, does not require accurate numerical integration over the input space and is not limited to GPs with squared exponential kernels. We evaluate our approach on synthetic and real-world data showing that its benefits are particularly pronounced on multivariate input settings where it overcomes the limitations of mean-field methods and sampling schemes. We provide the state of-the-art in terms of speed, accuracy and uncertainty quantification trade-offs.
翻译:我们提出一个可伸缩的框架,用于在一种由连续的模拟式Cox进程模型构建的、假定相应强度功能的不相容的 Poisson 进程中进行推断。 我们提出一个可伸缩的框架。 我们提出一个可伸缩的框架,这个框架的模型以连续的Sigmodal Cox 进程为模型中一个不相容的 Poisson 进程为模型,该过程假设相应的强度功能是由一个Gossian 进程(GP) 以规模化的后勤类小行星函数来给定的。 我们提出一个可伸缩的通过扩增和Poisson 进程来表示的可能性。 这个观点使得一个结构化的变异近似近似能够捕捉到模型中各变量之间的依赖性。 我们的框架避免了域的分散,不需要输入空间的精确数字整合,而不限于带有正方形指数内核的GPs。 我们评估了我们关于合成和真实世界数据的方法,显示其效益在多变量输入环境中特别显著,因为它克服了中平均方法和取样方法的局限性。 我们提供了速度、准确性和不确定性的权衡交易的状态。
相关内容
Source: Apple - iOS 8