Drift vs Shift: Decoupling Trends and Changepoint Analysis

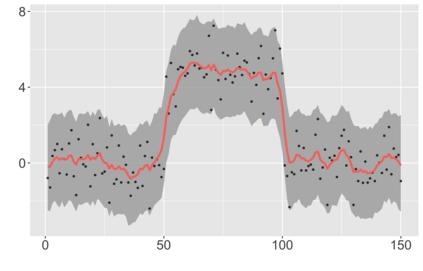
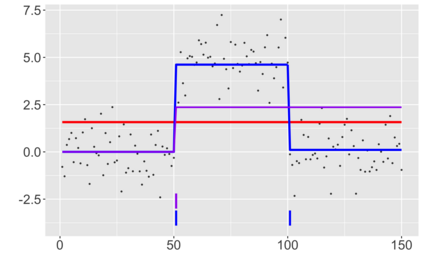
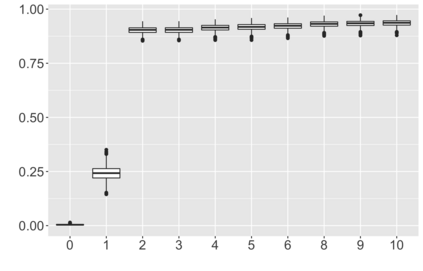
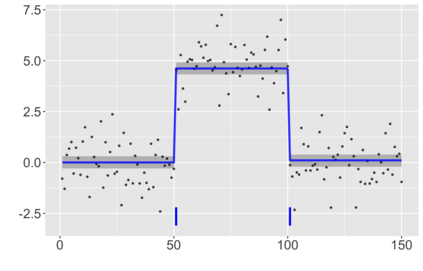
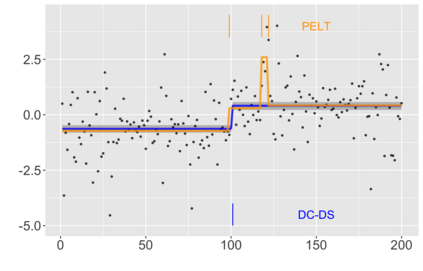
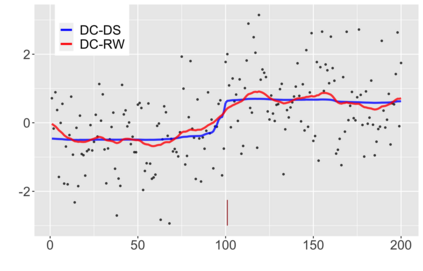
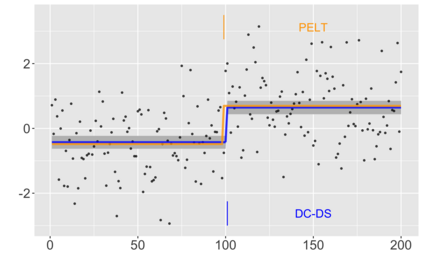
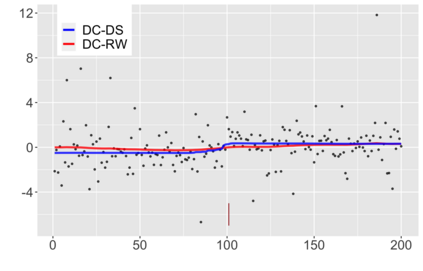
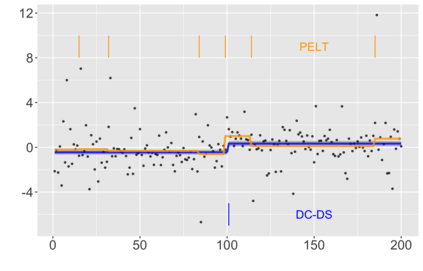
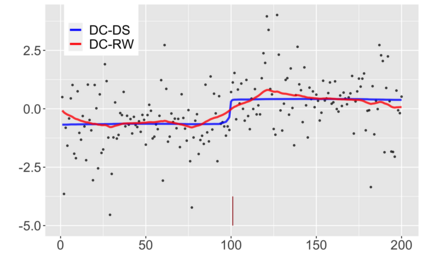
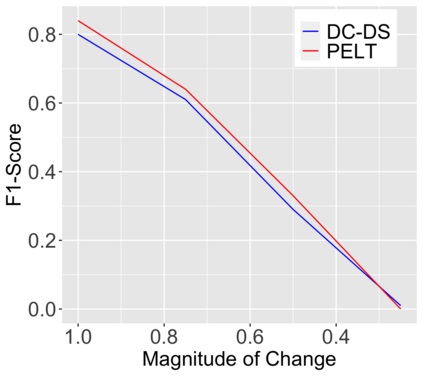
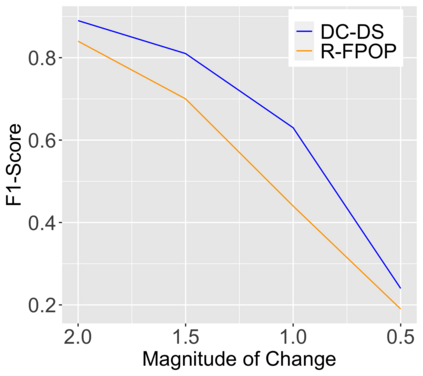
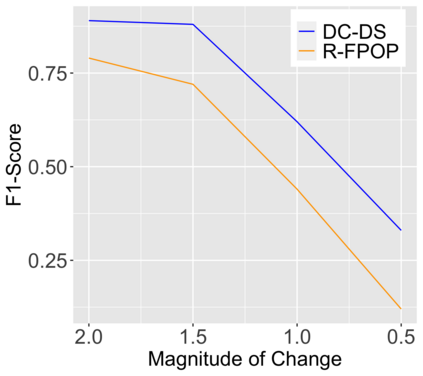
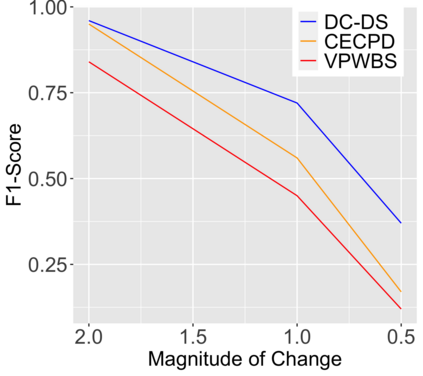
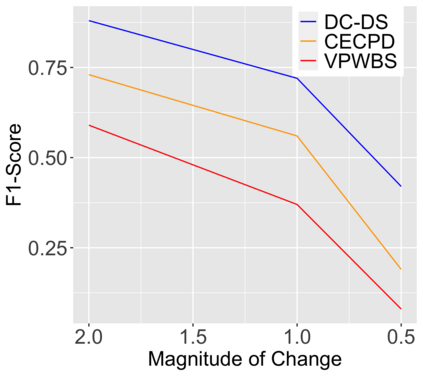
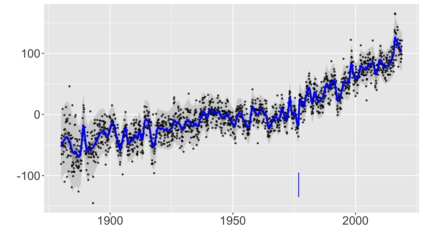
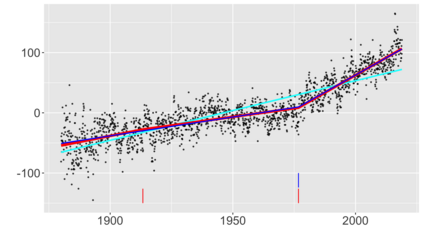
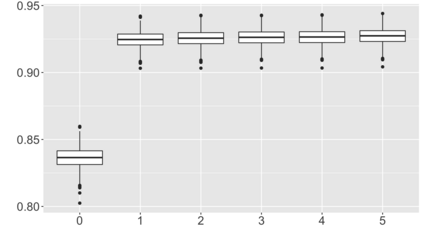
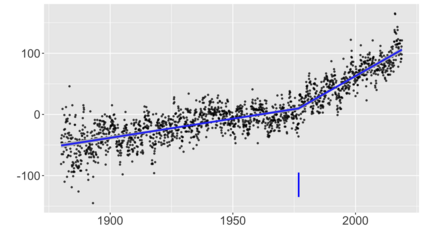
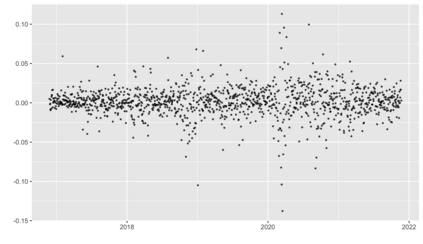
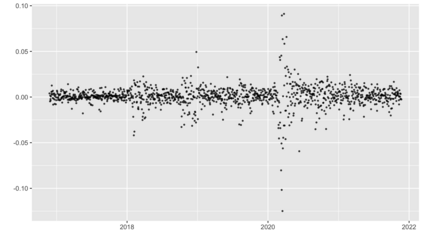
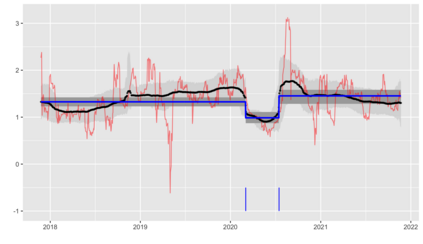
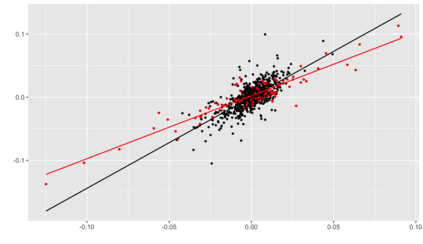
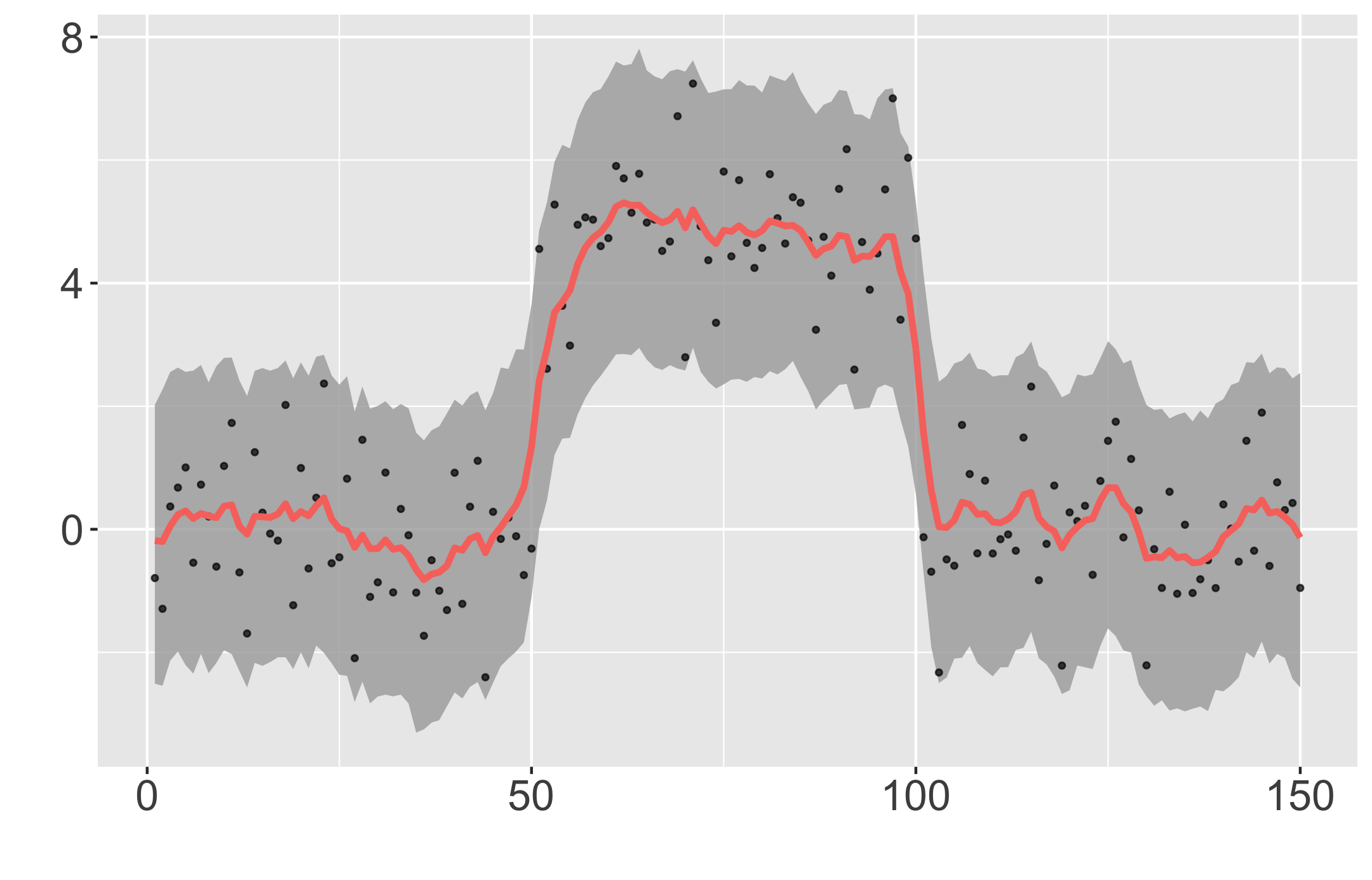
We introduce a new approach for decoupling trends (drift) and changepoints (shifts) in time series. Our locally adaptive model-based approach for robustly decoupling combines Bayesian trend filtering and machine learning based regularization. An over-parameterized Bayesian dynamic linear model (DLM) is first applied to characterize drift. Then a weighted penalized likelihood estimator is paired with the estimated DLM posterior distribution to identify shifts. We show how Bayesian DLMs specified with so-called shrinkage priors can provide smooth estimates of underlying trends in the presence of complex noise components. However, their inability to shrink exactly to zero inhibits direct changepoint detection. In contrast, penalized likelihood methods are highly effective in locating changepoints. However, they require data with simple patterns in both signal and noise. The proposed decoupling approach combines the strengths of both, i.e.\ the flexibility of Bayesian DLMs with the hard thresholding property of penalized likelihood estimators, to provide changepoint analysis in complex, modern settings. The proposed framework is outlier robust and can identify a variety of changes, including in mean and slope. It is also easily extended for analysis of parameter shifts in time-varying parameter models like dynamic regressions. We illustrate the flexibility and contrast the performance and robustness of our approach with several alternative methods across a wide range of simulations and application examples.