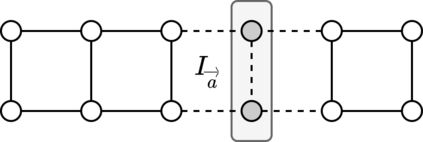
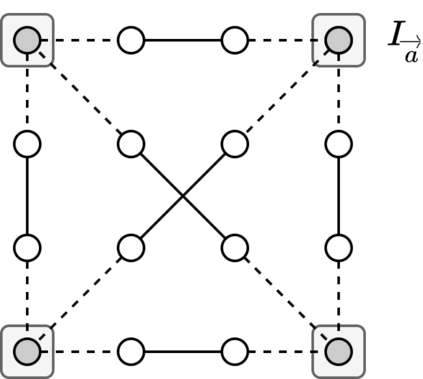
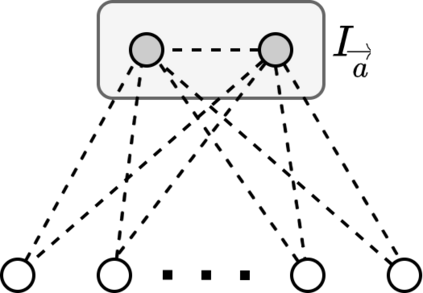
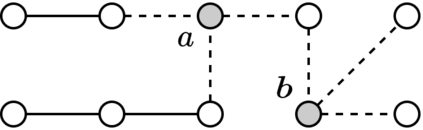
We analyze a game-theoretic abstraction of epidemic containment played on an undirected graph $G$: each player is associated with a node in $G$ and can either acquire protection from a contagious process or risk infection. After decisions are made, an infection starts at a random node $v$ and propagates through all unprotected nodes reachable from $v$. It is known that the price of anarchy (PoA) in $n$-node graphs can be as large as $\Theta(n)$. Our main result is a tight bound of order $\sqrt{n\Delta}$ on the PoA, where $\Delta$ is the maximum degree of the graph. We also study additional factors that can reduce the PoA, such as higher thresholds for contagion and varying the costs of becoming infected vs. acquiring protection.
翻译:暂无翻译
相关内容
Arxiv
0+阅读 · 2023年6月7日
Arxiv
0+阅读 · 2023年6月7日
Arxiv
0+阅读 · 2023年6月5日
Arxiv
34+阅读 · 2022年6月30日
Arxiv
13+阅读 · 2020年12月14日