Concentration inequalities and optimal number of layers for stochastic deep neural networks

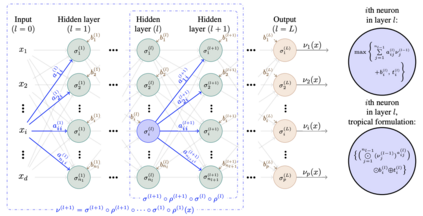
We state concentration and martingale inequalities for the output of the hidden layers of a stochastic deep neural network (SDNN), as well as for the output of the whole SDNN. These results allow us to introduce an expected classifier (EC), and to give probabilistic upper bound for the classification error of the EC. We also state the optimal number of layers for the SDNN via an optimal stopping procedure. We apply our analysis to a stochastic version of a feedforward neural network with ReLU activation function.