Efficient Accuracy Prediction for Differentially Private Algorithms

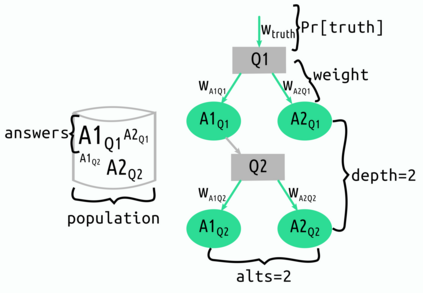
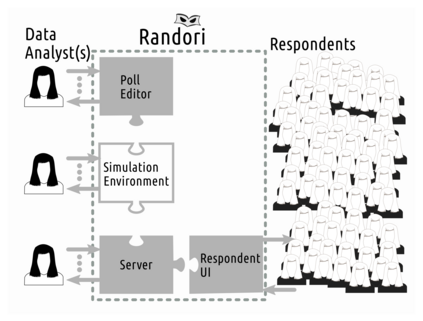
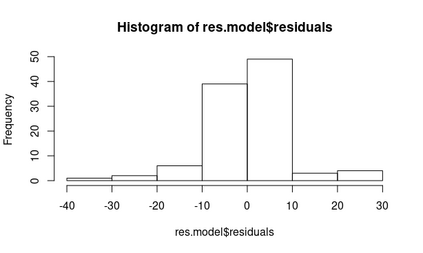
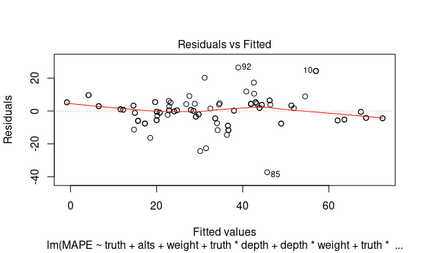
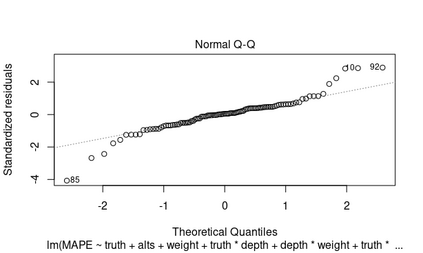
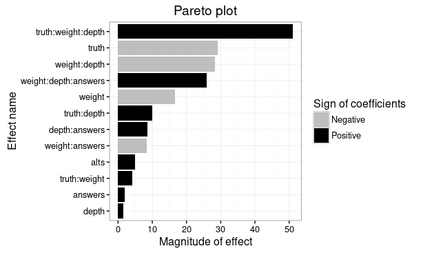
Differential privacy is a strong mathematical notion of privacy. Still, a prominent challenge when using differential privacy in real data collection is understanding and counteracting the accuracy loss that differential privacy imposes. As such, the accuracy-privacy trade-off of differential privacy needs to be balanced on a case-by-case basis. Applications in the literature tend to focus solely on analytical accuracy bounds, not include data in error prediction, or use arbitrary settings to measure error empirically. To fill the gap in the literature, we propose a novel application of factor experiments to create data aware error predictions. Basically, factor experiments provide a systematic approach to conducting empirical experiments. To demonstrate our methodology in action, we conduct a case study where error is dependent on arbitrarily complex tree structures. We first construct a tool to simulate poll data. Next, we use our simulated data to construct a least squares model to predict error. Last, we show how to validate the model. Consequently, our contribution is a method for constructing error prediction models that are data aware.