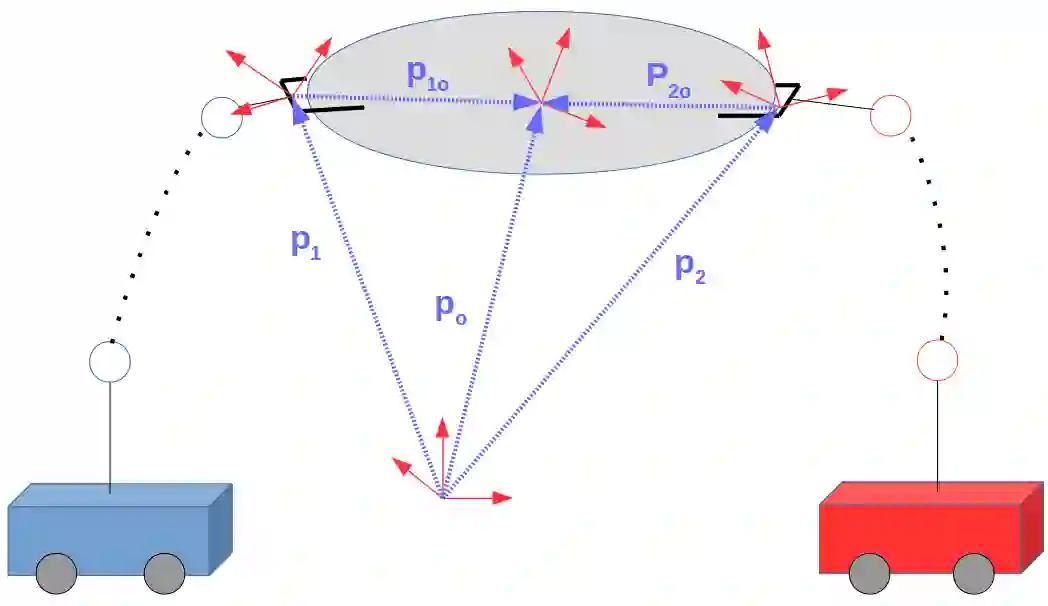
This paper considers the integration of rigid cooperative manipulation with rigidity theory. Motivated by rigid models of cooperative manipulation systems, i.e., where the grasping contacts are rigid, we introduce first the notion of bearing and distance rigidity for graph frameworks in SE(3). Next, we associate the nodes of these frameworks to the robotic agents of rigid cooperative manipulation schemes and we express the object-agent interaction forces by using the graph rigidity matrix, which encodes the infinitesimal rigid body motions of the system. Moreover, we show that the associated cooperative manipulation grasp matrix is related to the rigidity matrix via a range-nullspace relation, based on which we provide novel results on the relation between the arising interaction and internal forces and consequently on the energy-optimal force distribution on a cooperative manipulation system. Finally, simulation results on a realistic environment enhance the validity of the theoretical findings.
翻译:本文考虑将僵硬的合作操纵与僵硬的理论结合起来。在僵硬的合作操纵系统模式,即僵硬的握手接触时,我们首先为SE(3)中的图表框架引入带和距离僵硬的概念。接下来,我们将这些框架的节点与僵硬的合作操纵计划的机器人代理器联系起来,我们用图形僵硬的矩阵表达物体-试剂相互作用的力量,该矩阵将系统无限的僵硬体动作编码起来。此外,我们表明,相关的合作操纵掌握矩阵通过射线核空间关系与僵硬矩阵相联系,我们在此基础上就正在形成的相互作用与内部力量之间的关系以及随后在合作操纵系统中的能源最佳力量分布提供了新的结果。最后,在现实环境中的模拟结果加强了理论结论的有效性。