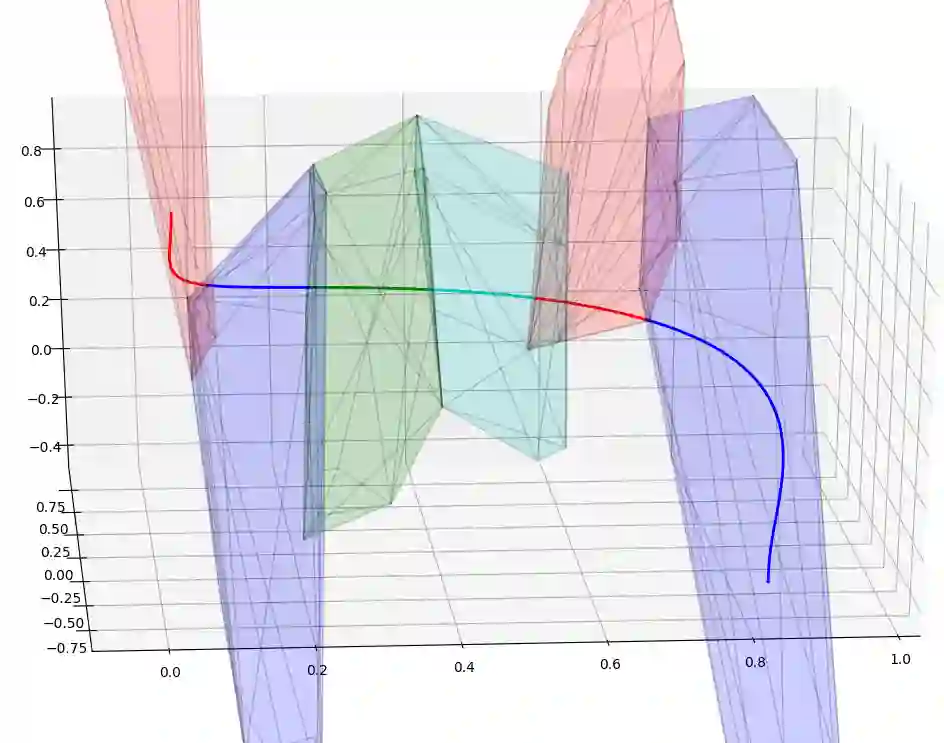
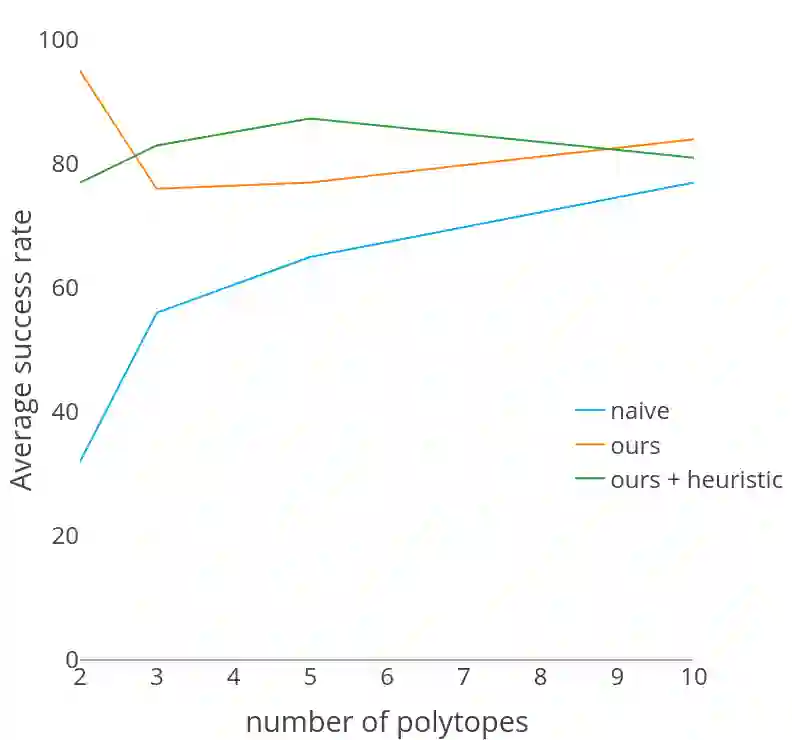
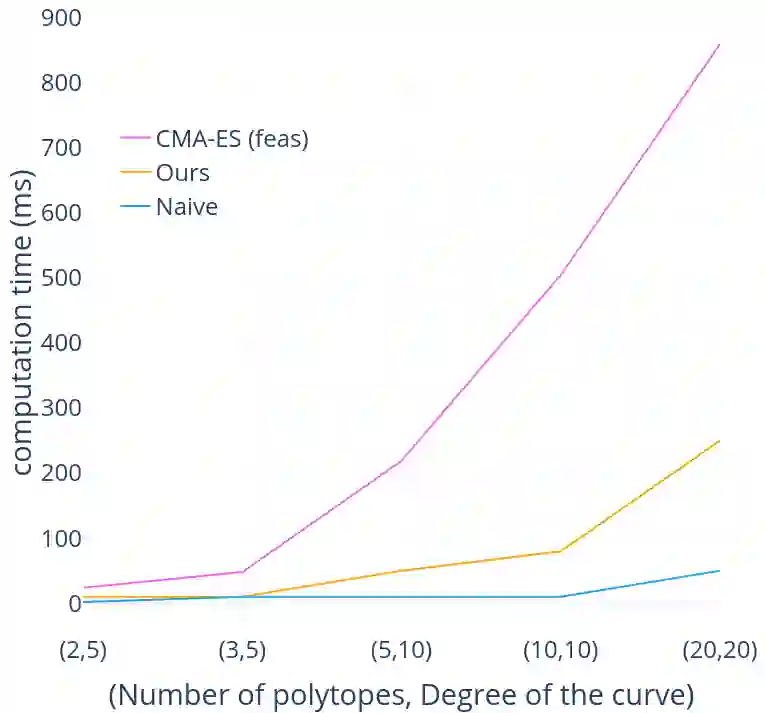
Non-linear Trajectory Optimisation (TO) methods require good initial guesses to converge to a locally optimal solution. A feasible guess can often be obtained by allocating a large amount of time for the trajectory to complete. However for unstable dynamical systems such as humanoid robots, this quasi-static assumption does not always hold. We propose a conservative formulation of the TO problem that simultaneously computes a feasible path and its time allocation. The problem is solved as an efficient convex optimisation problem guaranteed to converge to a locally optimal solution. The interest of the approach is illustrated with the computation of feasible trajectories that traverse sequentially a sequence of polytopes. We demonstrate that on instances of the problem where the quasi static solutions are not admissible, our approach is able to find a feasible solution with a success rate above $80 \%$ in all the scenarios considered, in less than 10ms for problems involving traversing less than 5 polytopes and less than 1s for problems involving 20 polytopes, thus demonstrating its ability to reliably provide initial guesses to advanced non linear solvers.
翻译:非线性轨迹优化(TO)方法需要良好的初步猜想,以便汇合到一个当地最佳的解决方案。 通常可以通过为轨迹的完成分配大量时间来获得可行的猜想。 但是,对于人类机器人等不稳定的动态系统来说,这种准静态假设并不总能站住脚。 我们建议对问题进行保守的提法,同时计算可行的路径和时间分配。 问题作为高效的convex优化问题来解决,保证它与当地的最佳解决方案汇合。 这种方法的兴趣表现在对按顺序绕绕多面序列的可行轨迹的计算中。 我们证明,在准静态解决方案无法被接受的问题上,我们的方法能够找到一种可行的解决方案,在所考虑的所有情景中,成功率超过80 ⁇ 美元,对于涉及不超过5个多面的问题不超过10米,对于涉及20个多面的问题小于1米的问题,我们能够可靠地向先进的非线性解决方案提供初步猜测。