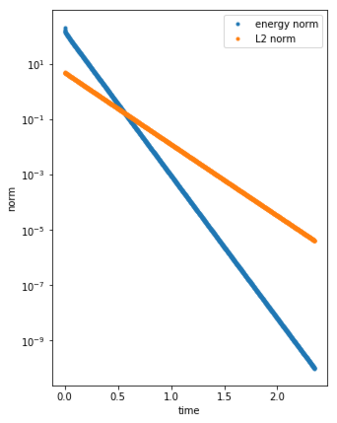
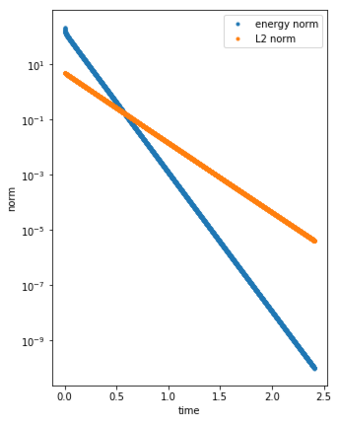
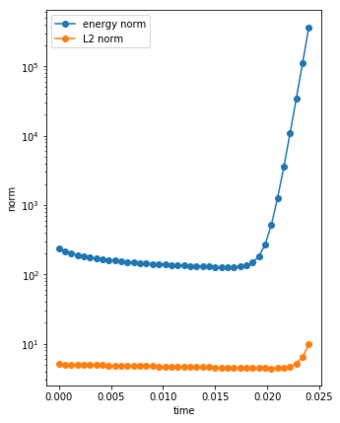
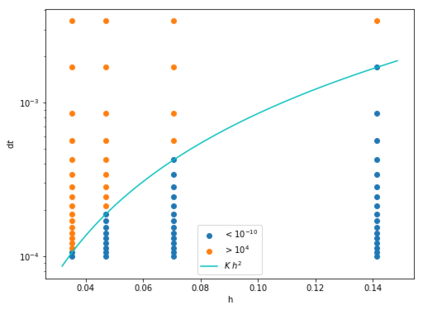
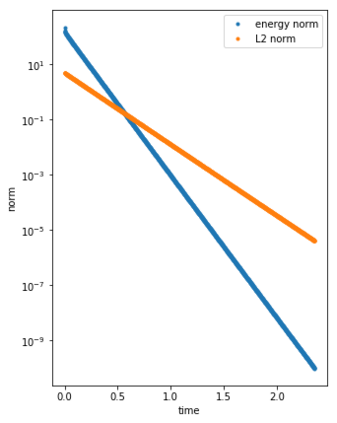
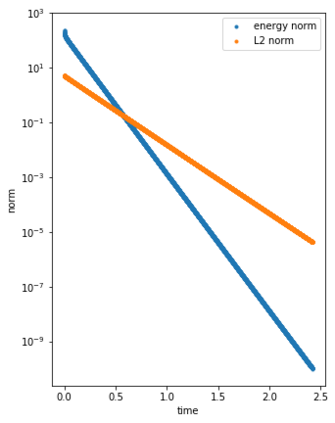
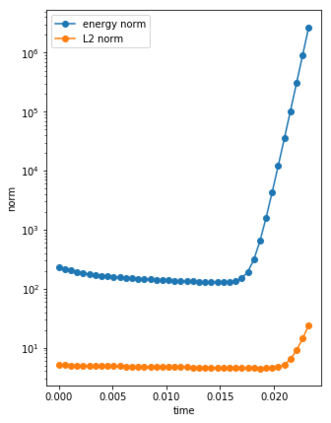
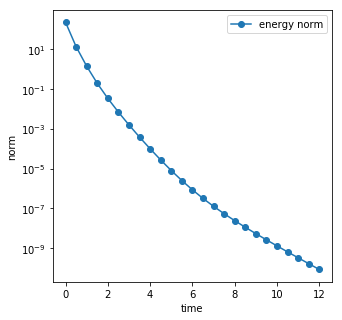
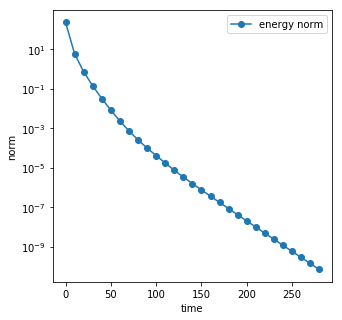
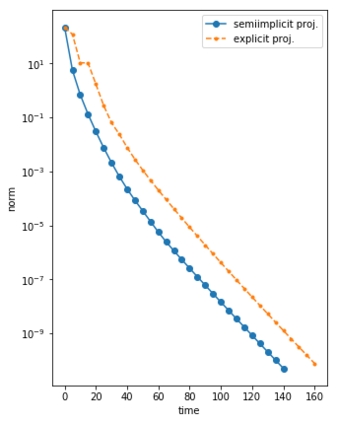
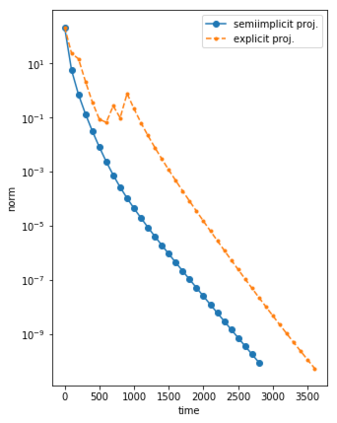
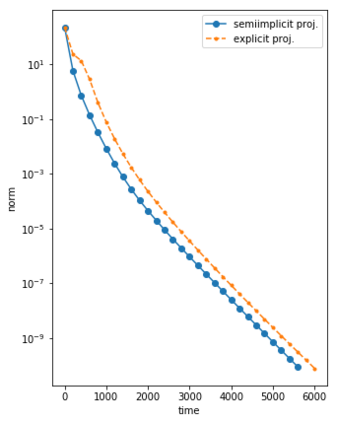
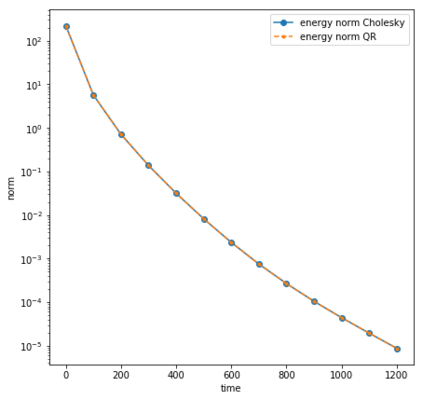
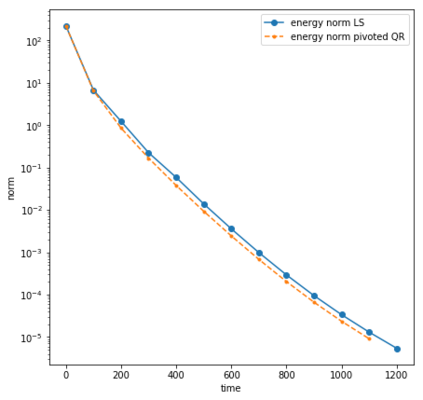
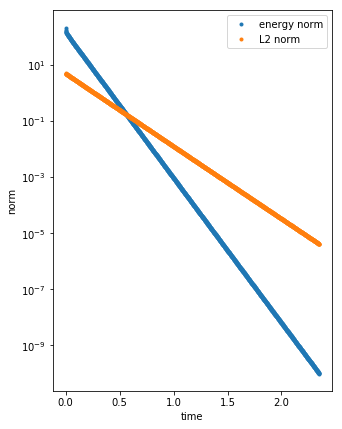
We consider the Dynamical Low Rank (DLR) approximation of random parabolic equations and propose a class of fully discrete numerical schemes. Similarly to the continuous DLR approximation, our schemes are shown to satisfy a discrete variational formulation. By exploiting this property, we establish stability of our schemes: we show that our explicit and semi-implicit versions are conditionally stable under a parabolic type CFL condition which does not depend on the smallest singular value of the DLR solution; whereas our implicit scheme is unconditionally stable. Moreover, we show that, in certain cases, the semi-implicit scheme can be unconditionally stable if the randomness in the system is sufficiently small. Furthermore, we show that these schemes can be interpreted as projector-splitting integrators and are strongly related to the scheme proposed by Lubich et al. [BIT Num. Math., 54:171-188, 2014; SIAM J. on Num. Anal., 53:917-941, 2015], to which our stability analysis applies as well. The analysis is supported by numerical results showing the sharpness of the obtained stability conditions.
翻译:我们认为随机抛物线方程式的动态低端近似值(DLR)是随机抛物线方程式的动态低端近似值,并提出了一组完全独立的数字方案。与连续的DLR近似值相似,我们的计划显示能够满足离散的变异配方。我们通过利用这一属性来建立我们的计划的稳定性:我们表明,我们的明确和半隐含的版本在一种不取决于DLR解决方案最小单值的抛物线式CFL(DLR)条件下有条件稳定;而我们的隐含计划是无条件稳定的。此外,我们表明,在某些情况下,如果系统中的随机性足够小,半隐含性计划可以无条件稳定。此外,我们表明,这些计划可以被解释为投射或分裂的集成体,并且与Lubich等人提议的计划密切相关。 [BIT Num. Math., 54:171-188,2014;SIM J. on Num. Anal., 53:917-941,2015],我们的稳定分析也适用于它。我们的分析得到数字结果的支持,以显示获得的稳定性条件的精确性。