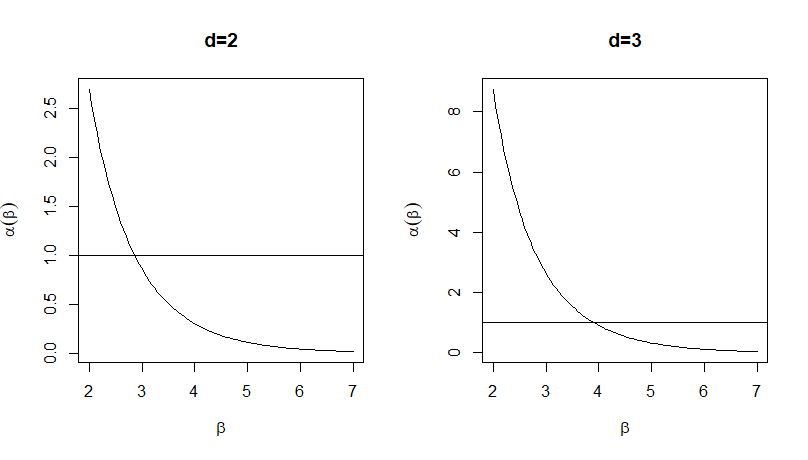
We consider a Random Graph Model on $\mathbb{Z}^{d}$ that incorporates the interplay between the statistics of the graph and the underlying space where the vertices are located. Based on a graphical construction of the model as the invariant measure of a birth and death process, we prove the existence and uniqueness of a measure defined on graphs with vertices in $\mathbb{Z}^{d}$ which coincides with the limit along the measures over graphs with finite vertex set. As a consequence, theoretical properties such as exponential mixing of the infinite volume measure and central limit theorem for averages of a real-valued function of the graph are obtained. Moreover, a perfect simulation algorithm based on the clan of ancestors is described in order to sample a finite window of the equilibrium measure defined on $\mathbb{Z}^{d}$.
翻译:我们考虑用$\mathb ⁇ d}$(mathb ⁇ d}$)的随机图表模型,该模型将图形统计数据与顶部所在空间之间的相互作用纳入其中。根据模型的图形构造作为出生和死亡过程的不变测量标准,我们证明用$(mathb ⁇ d}$($)的顶部的图表定义的测量标准的存在和独特性,该标准与用有限的顶部设置的图形测量标准相比的极限相吻合。因此,获得了一些理论属性,如无限量测量指数的指数混合和图中实际价值函数平均值的中心限值。此外,还描述了基于祖先氏族的完美模拟算法,以抽样用$(mathb ⁇ d}$($)定义的平衡测量标准的一个有限窗口。