Predicting trajectory behaviour via machine-learned invariant manifolds

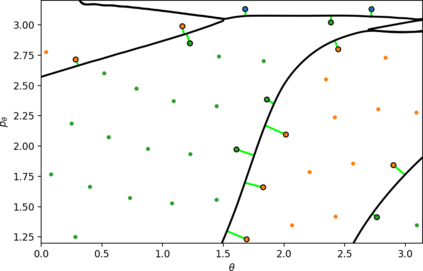
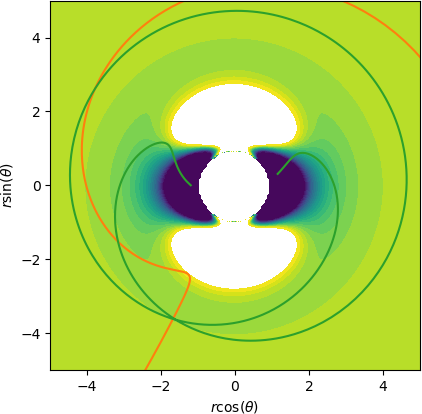
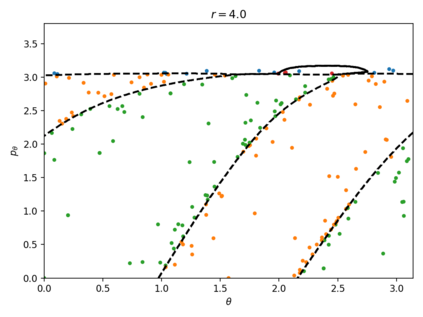
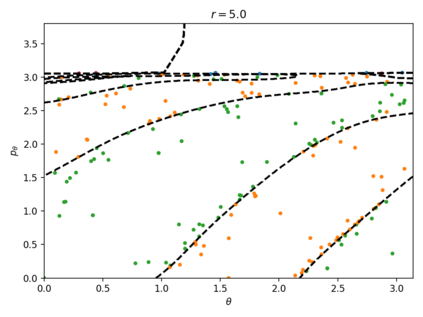
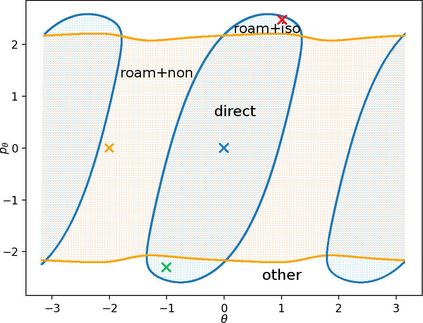
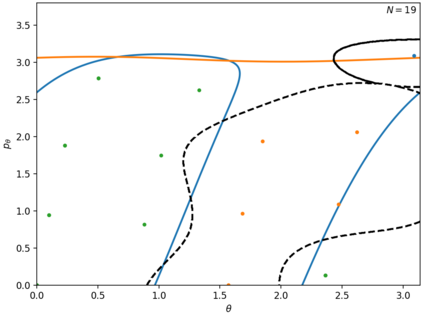
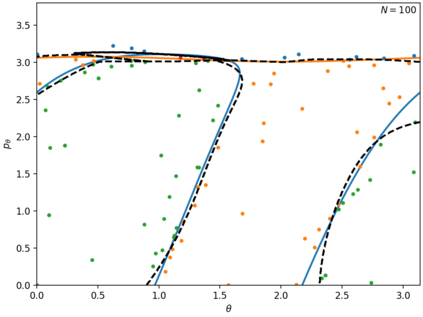
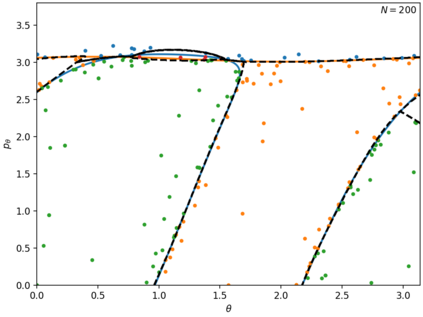
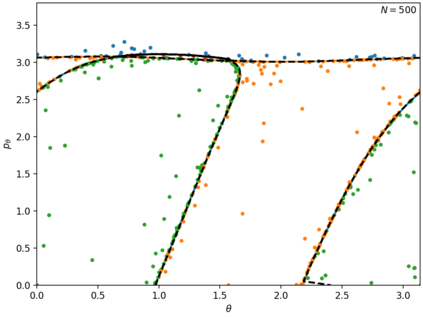
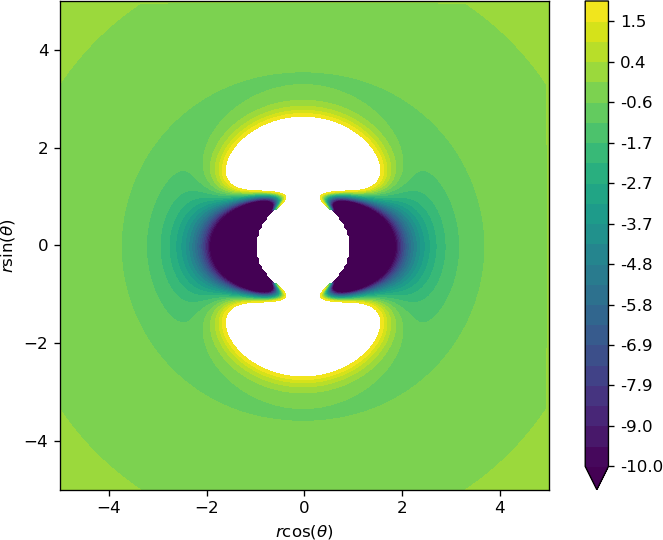
In this paper we use support vector machines (SVM) to develop a machine learning framework to discover the phase space structure that can distinguish between distinct reaction pathways. The machine learning model is trained using data from trajectories of Hamilton's equations but lends itself for use in molecular dynamics simulation. The framework is specifically designed to require minimal a priori knowledge of the dynamics in a system. We benchmark our approach with a model Hamiltonian for the reaction of an ion and a molecule due to Chesnavich consisting of two parts: a rigid, symmetric top representing the $\text{CH}_3^{+}$ ion, and a mobile $\text{H}$ atom. We begin with trajectories and use support vector machines to determine the boundaries between initial conditions corresponding to different classes of trajectories. We then show that these boundaries between different classes of trajectories approximate invariant phase space structures of the same type observed in earlier analyses of Chesnavich's model. Our approach is designed with extensions to higher-dimensional applications in mind. SVM is known to work well even with small amounts of data, therefore our approach is computationally better suited than existing methods for high-dimensional systems and systems where integrating trajectories is expensive.