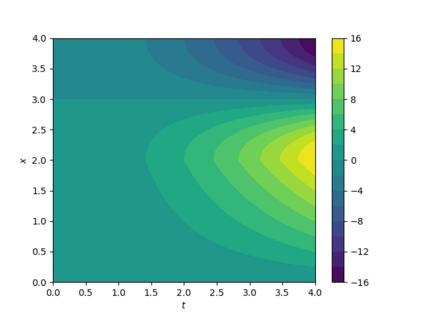
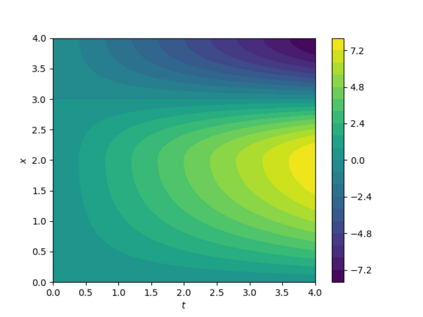
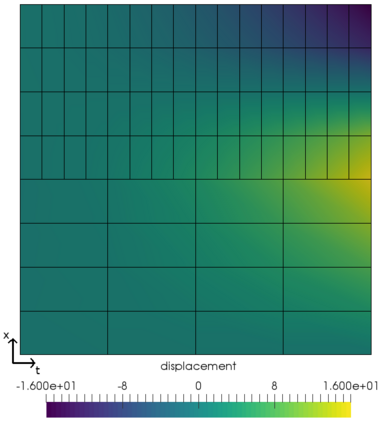
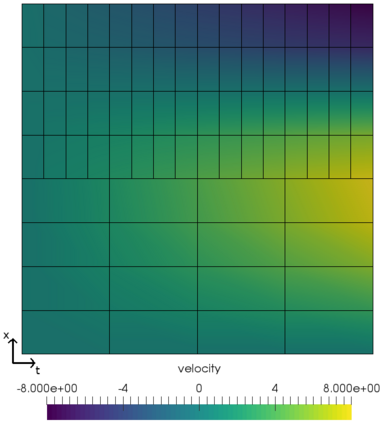
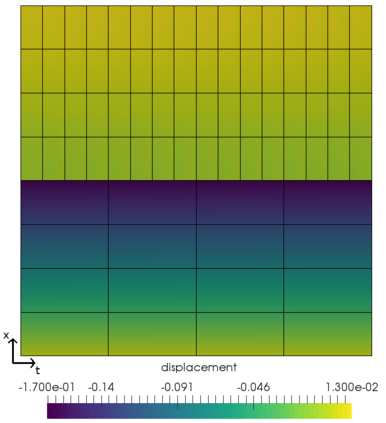
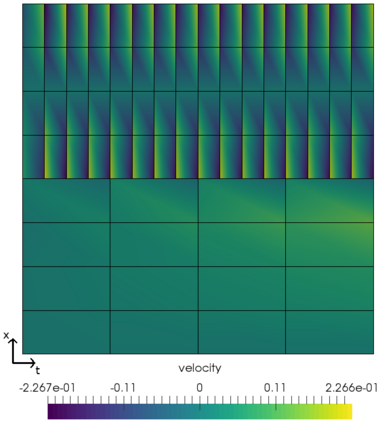
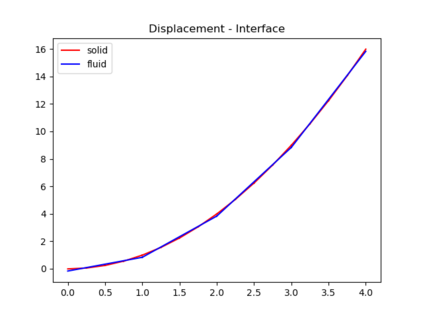
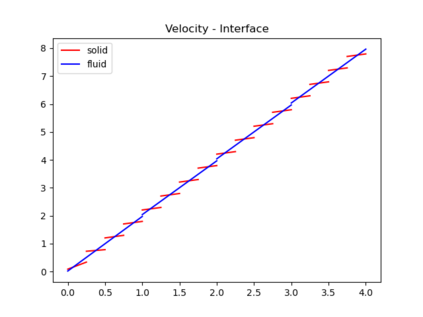
In this work, we propose and computationally investigate a monolithic space-time multirate scheme for coupled problems. The novelty lies in the monolithic formulation of the multirate approach as this requires a careful design of the functional framework, corresponding discretization, and implementation. Our method of choice is a tensor-product Galerkin space-time discretization. The developments are carried out for both prototype interface- and volume coupled problems such as coupled wave-heat-problems and a displacement equation coupled to Darcy flow in a poro-elastic medium. The latter is applied to the well-known Mandel's benchmark and a three-dimensional footing problem. Detailed computational investigations and convergence analyses give evidence that our monolithic multirate framework performs well.
翻译:暂无翻译