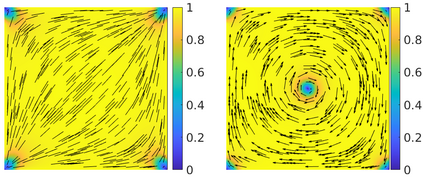
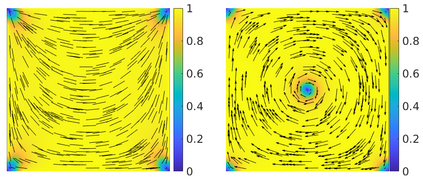
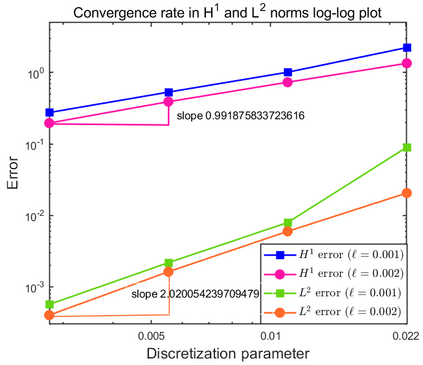
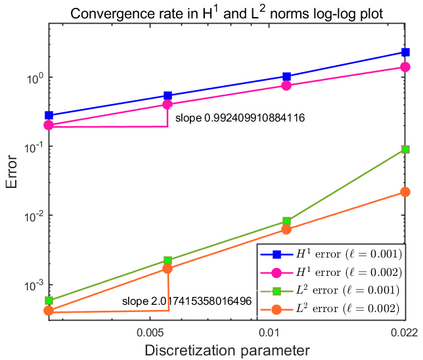
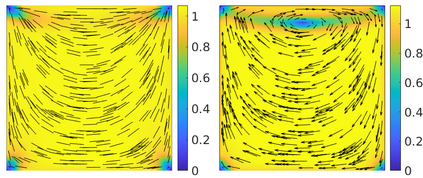
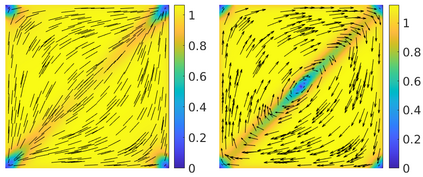
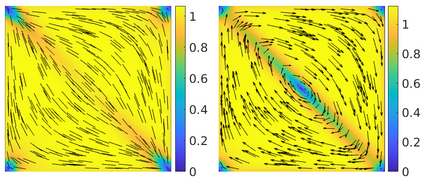
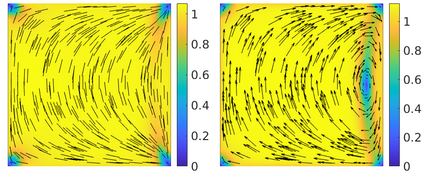
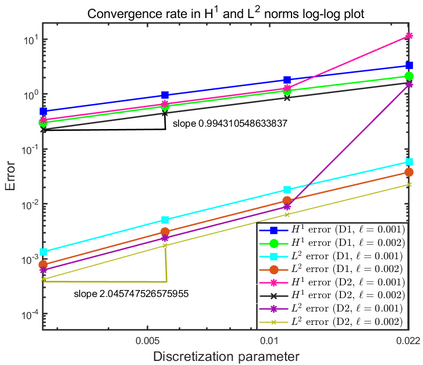
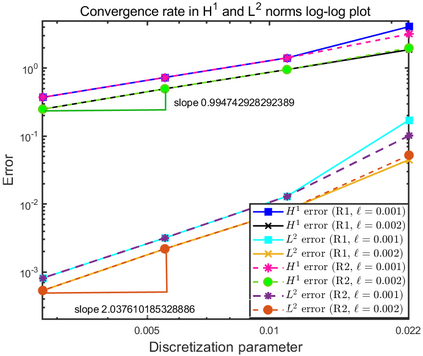
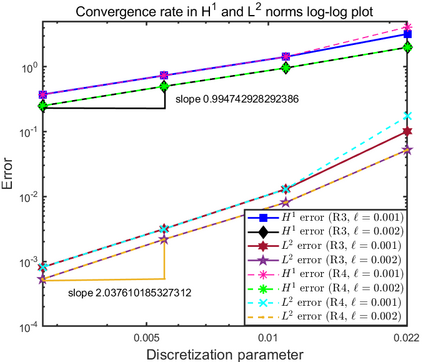
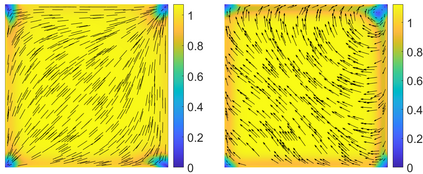
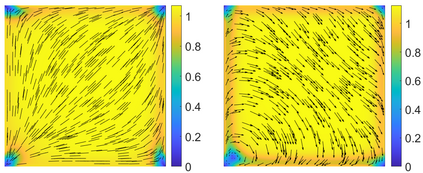
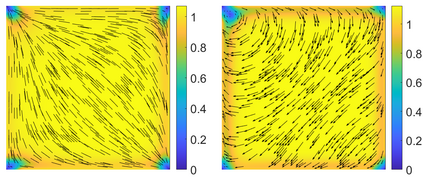
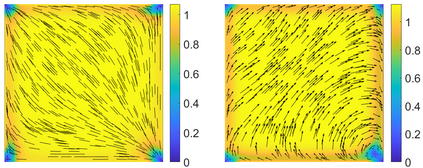
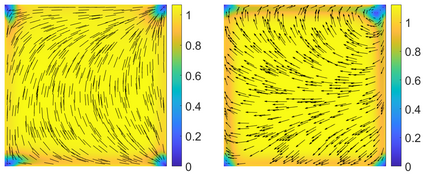
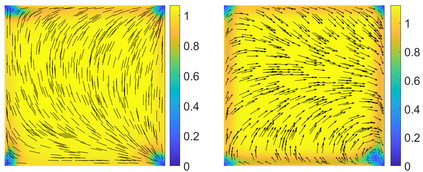
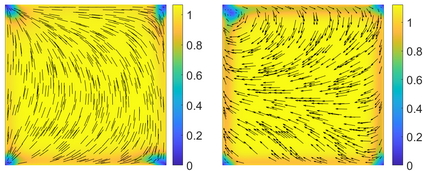
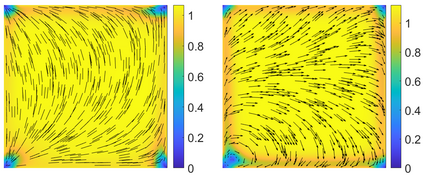
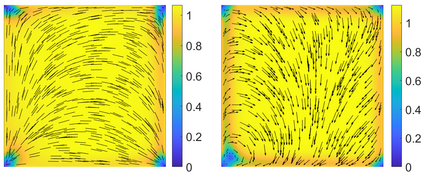
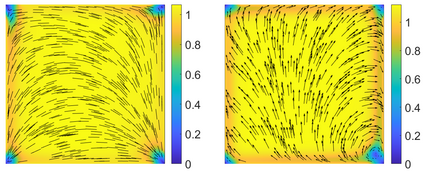
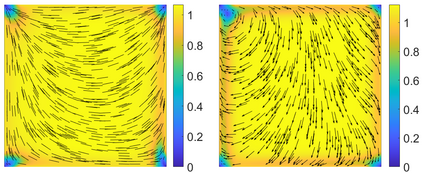
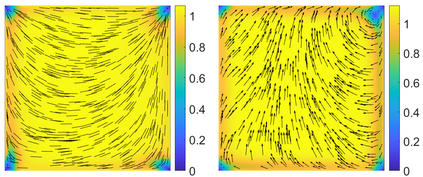
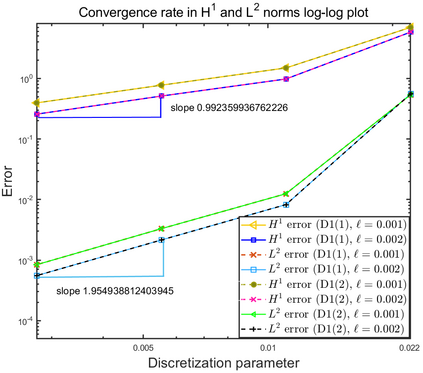
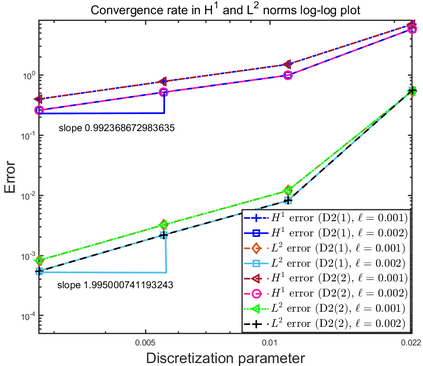
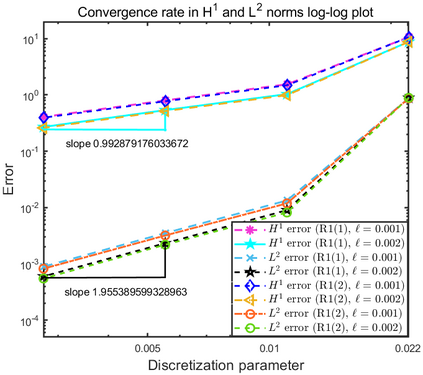
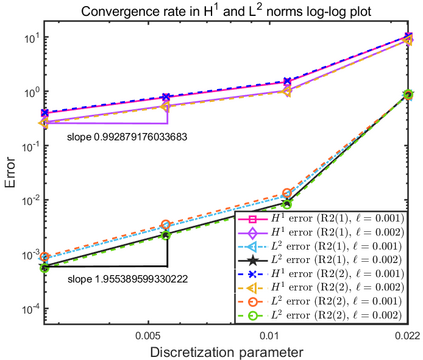
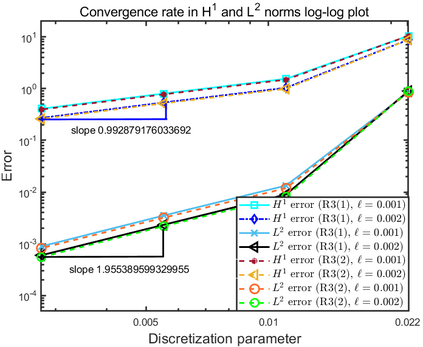
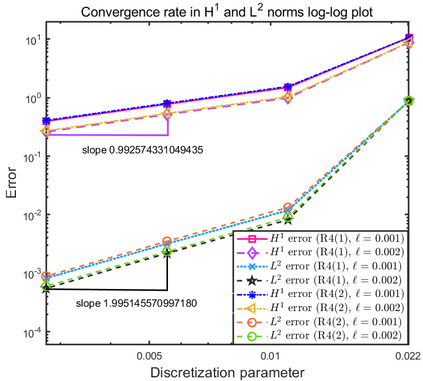
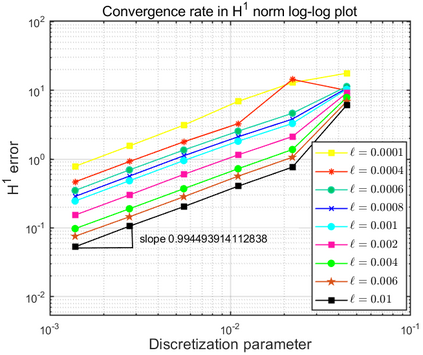
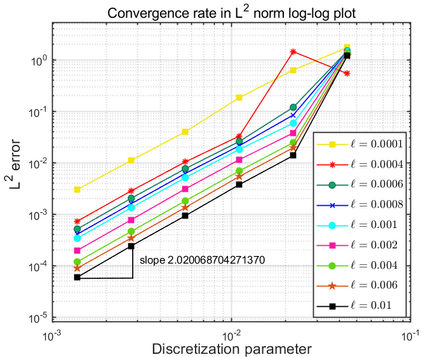
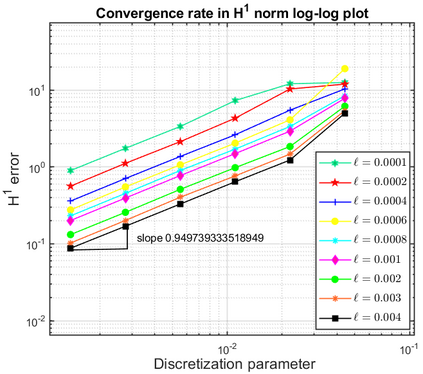
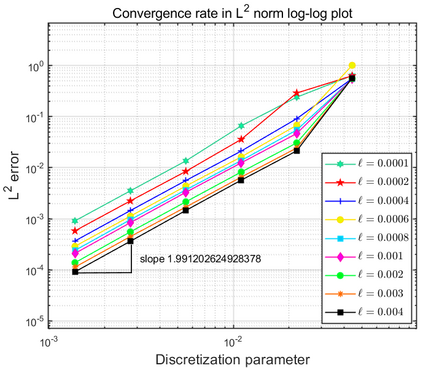
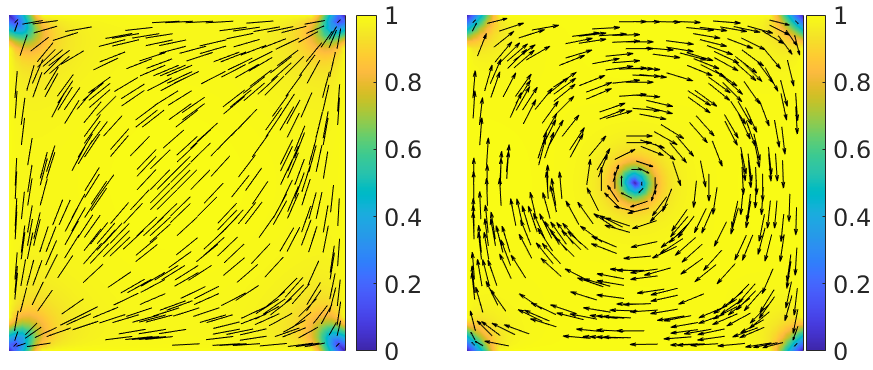
This paper focuses on the analysis of a free energy functional, that models a dilute suspension of magnetic nanoparticles in a two-dimensional nematic well. The {\it first part} of the article is devoted to the asymptotic analysis of global energy minimizers in the limit of vanishing elastic constant, $\ell \rightarrow 0$ where the re-scaled elastic constant $\ell$ is inversely proportional to the domain area. The first results concern the strong $H^1$-convergence and a $\ell$-independent $H^2$-bound for the global minimizers on smooth bounded 2D domains, with smooth boundary and topologically trivial Dirichlet conditions. The {\it second part} focuses on the discrete approximation of regular solutions of the corresponding non-linear system of partial differential equations with cubic non-linearity and non-homogeneous Dirichlet boundary conditions. We establish (i) the existence and local uniqueness of the discrete solutions using fixed point argument, (ii) a best approximation result in energy norm, (iii) error estimates in the energy and $L^2$ norms with $\ell $- discretization parameter dependency for the conforming finite element method. Finally, the theoretical results are complemented by numerical experiments on the discrete solution profiles, the numerical convergence rates that corroborates the theoretical estimates, followed by plots that illustrate the dependence of the discretization parameter on $\ell$.
翻译:本文侧重于对自由能源功能的分析, 即磁纳米粒子在二维线性油井中稀释磁纳米粒子的悬浮。 文章的 {it 第一部分} 用于对全球能源最小化器进行无症状分析, 其极限是消失弹性常数, $\ ell\ rightrow 0$, 其重新缩放弹性常数 $\ ell 与域域成反比。 第一个结果涉及强的H1美元- covergation 和 美元- 美元- 美元- 美元- 独立 美元- 美元- 基数在平滑的2D 域全球最小化器上, 其特点是平滑的边界和表面的微不足道的 Dirichlet 条件。 ~ 第二部分 侧重于相应的非线性差化部分等式公式的常规近似值, 即与立线性和非相异性差的边界条件成反比。 我们确定(i) 使用固定点参数参数的离散解决方案的存在和本地独特性 $2美元-, (ii) 能源规范中最接近的结果, 美元-, 和表面的离差性标准的精确的轨值 值 度值 值 值 的精确值 值 和精确性 值 值 值 值 值 值 值 值 值 值 值 值 的 值 值 的 的 的 值 的 的 的 的 的 的 的 的 值 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 和 的 的 的 的 的 的 的 的 的 的