The Hurst roughness exponent and its model-free estimation

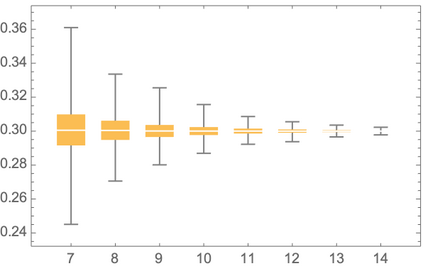
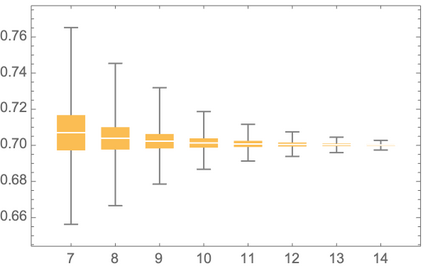
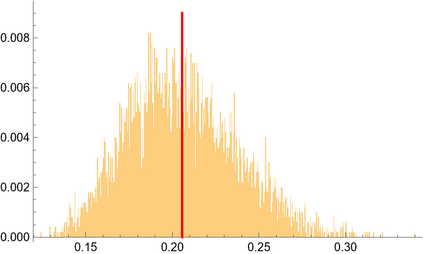
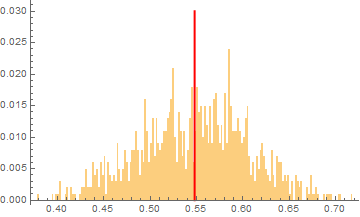
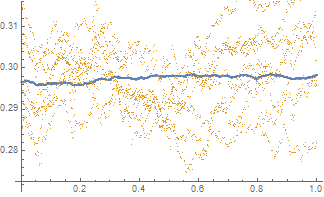
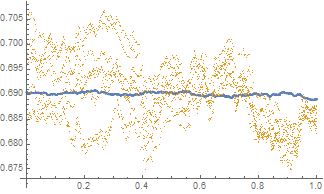
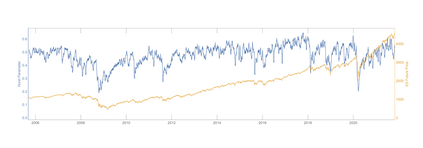
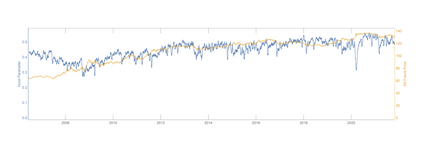
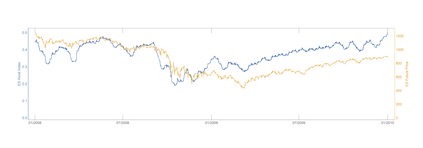
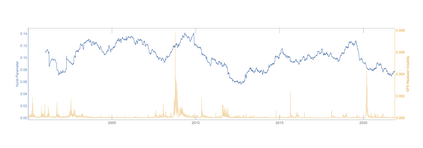
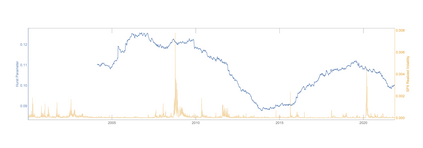
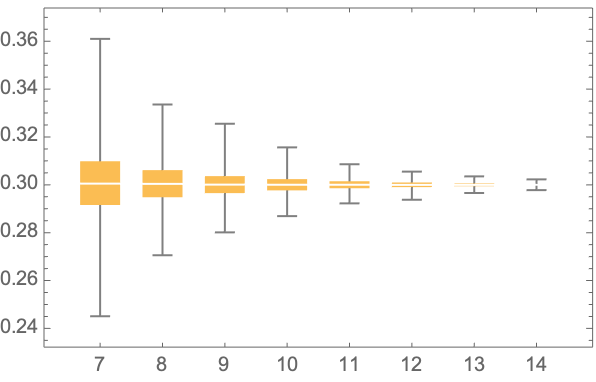
We say that a continuous real-valued function $x$ admits the Hurst roughness exponent $H$ if the $p^{\text{th}}$ variation of $x$ converges to zero if $p>1/H$ and to infinity if $p<1/H$. For the sample paths of many stochastic processes, such as fractional Brownian motion, the Hurst roughness exponent exists and equals the standard Hurst parameter. In our main result, we provide a mild condition on the Faber--Schauder coefficients of $x$ under which the Hurst roughness exponent exists and is given as the limit of the classical Gladyshev estimates $\wh H_n(x)$. This result can be viewed as a strong consistency result for the Gladyshev estimators in an entirely model-free setting, because no assumption whatsoever is made on the possible dynamics of the function $x$. Nonetheless, our proof is probabilistic and relies on a martingale that is hidden in the Faber--Schauder expansion of $x$. Since the Gladyshev estimators are not scale-invariant, we construct several scale-invariant estimators that are derived from the sequence $(\wh H_n)_{n\in\bN}$. We also discuss how a dynamic change in the Hurst roughness parameter of a time series can be detected. Our results are illustrated by means of high-frequency financial times series.