Approximate selective inference via maximum likelihood

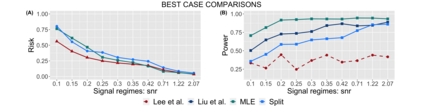
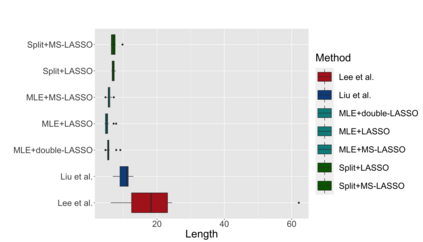
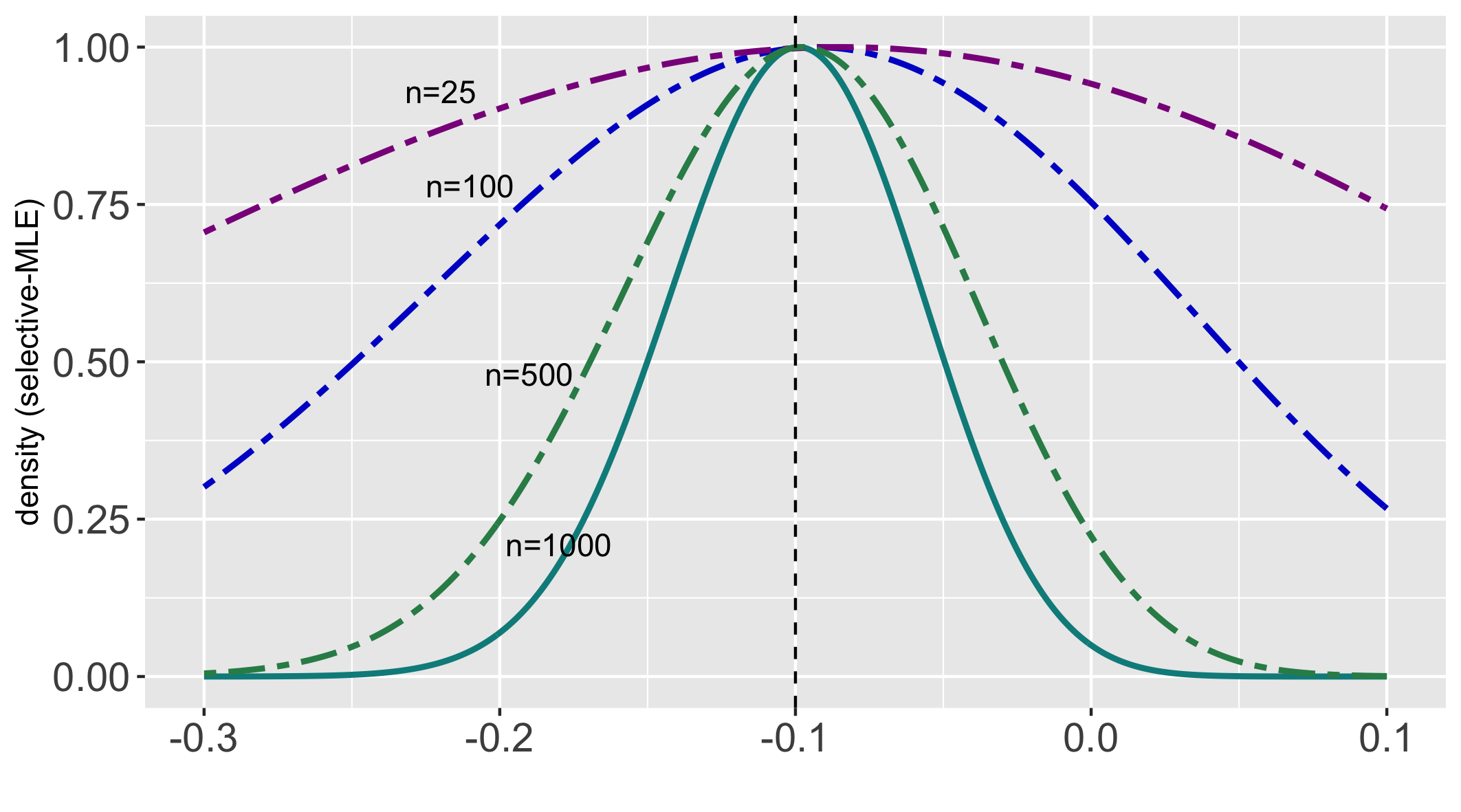
Several strategies have been developed recently to ensure valid inference after model selection; some of these are easy to compute, while others fare better in terms of inferential power. In this paper, we consider a selective inference framework for Gaussian data. We propose a new method for inference through approximate maximum likelihood estimation. Our goal is to: (i) achieve better inferential power with the aid of randomization, (ii) bypass expensive MCMC sampling from exact conditional distributions that are hard to evaluate in closed forms. We construct approximate inference, for e.g. p-values, confidence intervals etc., by solving a fairly simple, convex optimization problem. We illustrate the potential of our method across wide-ranging values of signal-to-noise ratio in simulations. On a cancer gene expression data set we find that our method improves upon the inferential power of some commonly used strategies for selective inference.