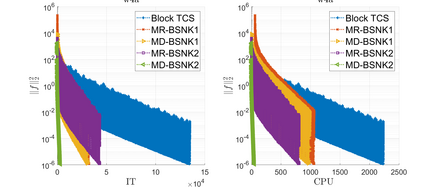
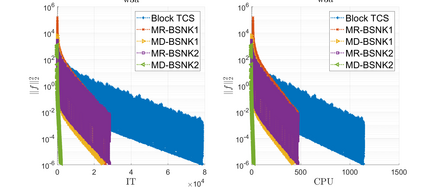
The nonlinear Kaczmarz method was recently proposed to solve the system of nonlinear equations. In this paper, we first discuss two greedy selection rules, i.e., the maximum residual and maximum distance rules, for the nonlinear Kaczmarz iteration. Then, based on them, two kinds of greedy randomized sampling methods are presented. Further, we also devise four corresponding greedy randomized block methods, i.e., the multiple samples-based methods. The linear convergence in expectation of all the proposed methods is proved. Numerical results show that, in some applications including brown almost linear function and generalized linear model, the greedy selection rules give faster convergence rates than the random ones, and the block methods outperform the single sample-based ones.
翻译:最近提出了非线性卡茨马尔兹方法以解决非线性方程式系统。 在本文中,我们首先讨论了两种贪婪的选择规则,即非线性卡茨马尔兹迭代的最大剩余和最大距离规则。然后,根据这些规则,提出了两种贪婪随机抽样方法。此外,我们还设计了四种相应的贪婪随机区块方法,即多个样本法。所有拟议方法的线性趋同得到了证明。数字结果显示,在一些应用中,包括棕色几乎线性函数和通用线性模型,贪婪选择规则比随机规则的趋同率更快,而区块方法优于单一样本法。