The average size of maximal matchings in graphs

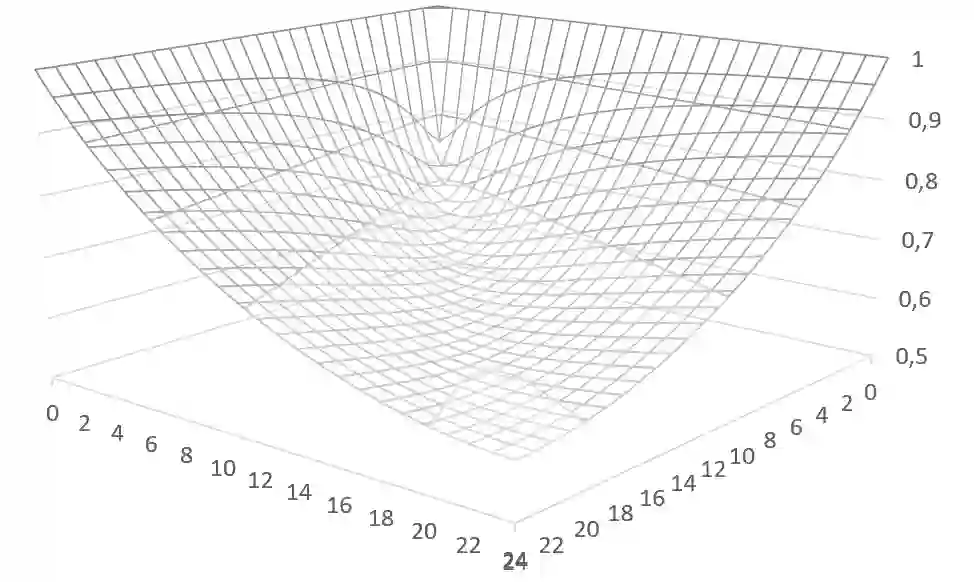
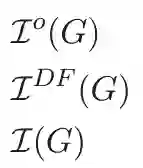We investigate the ratio $I(G)$ of the average size of a maximal matching to the size of a maximum matching in a graph $G$. If many maximal matchings have a size close to $\mu(G)$, this graph invariant has a value close to 1. Conversely, if many maximal matchings have a small size, $I(G)$ approaches $\frac{1}{2}$. We propose a general technique to determine the asymptotic behavior of $\avM(G)$ for various classes of graphs. To illustrate the use of this technique, we first show how it makes it possible to find known asymptotic values of $I(G)$ which were typically obtained using generating functions, and we then determine the asymptotic value of $I(G)$ for other families of graphs, highlighting the spectrum of possible values of this graph invariant between $\frac{1}{2}$ and $1$.