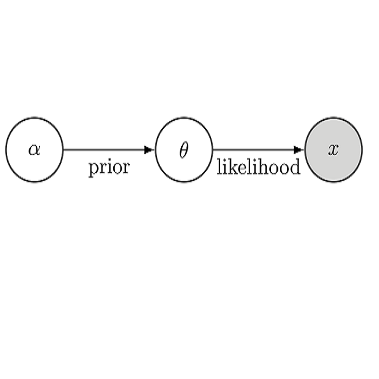
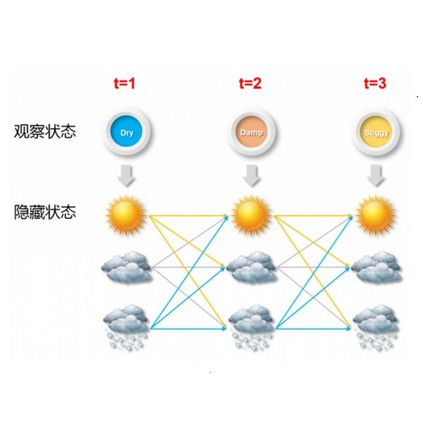
We consider the modeling of data generated by a latent continuous-time Markov jump process with a state space of finite but unknown dimensions. Typically in such models, the number of states has to be pre-specified, and Bayesian inference for a fixed number of states has not been studied until recently. In addition, although approaches to address the problem for discrete-time models have been developed, no method has been successfully implemented for the continuous-time case. We focus on reversible jump Markov chain Monte Carlo which allows the trans-dimensional move among different numbers of states in order to perform Bayesian inference for the unknown number of states. Specifically, we propose an efficient split-combine move which can facilitate the exploration of the parameter space, and demonstrate that it can be implemented effectively at scale. Subsequently, we extend this algorithm to the context of model-based clustering, allowing numbers of states and clusters both determined during the analysis. The model formulation, inference methodology, and associated algorithm are illustrated by simulation studies. Finally, We apply this method to real data from a Canadian healthcare system in Quebec.
翻译:我们认为,对由隐性连续时间的Markov跳跃过程产生的数据进行模型化,其状态空间有限,但范围未知。在这类模型中,典型的情况是,必须预先确定国家的数目,而且直到最近才对固定数目的国家的贝叶斯推论进行研究。此外,虽然已经制定了解决离散时间模型问题的方法,但没有为连续时间案例成功采用任何方法。我们侧重于可逆跳跃的Markov链子蒙特卡洛,允许不同数目的国家进行跨维移动,以便对数目不详的州进行巴伊西亚推论。具体地说,我们建议采取高效的分裂通信移动,以便利对参数空间的探索,并表明可以大规模有效地实施。随后,我们将这一算法扩大到基于模型的集群环境,允许在分析中确定国家和集群的数目。模拟研究对模型的拟订、推断方法和相关算法进行了说明。最后,我们将这一方法应用于魁北克加拿大保健系统的真实数据。