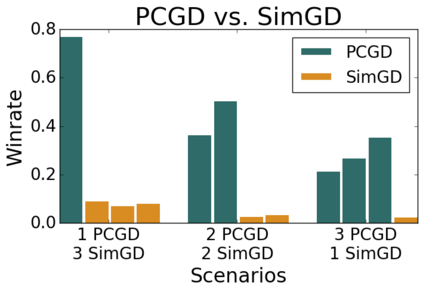
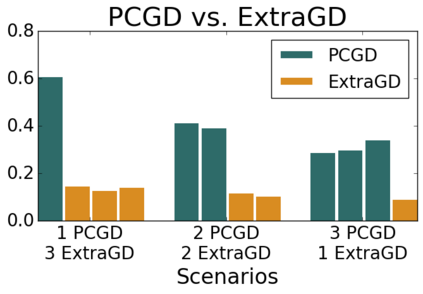
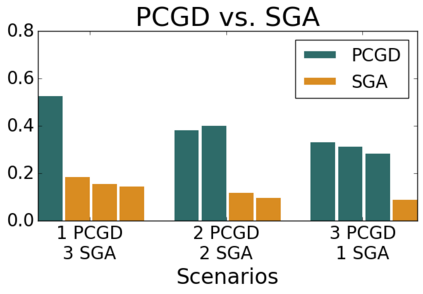
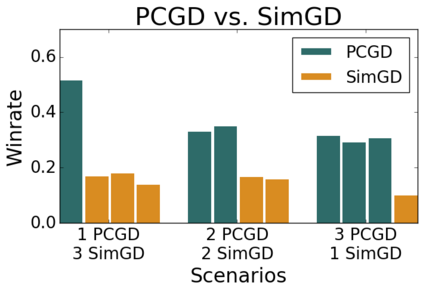
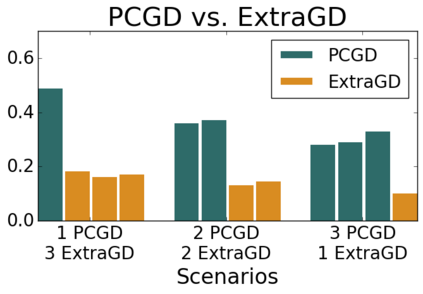
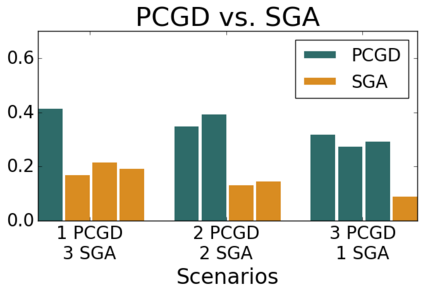
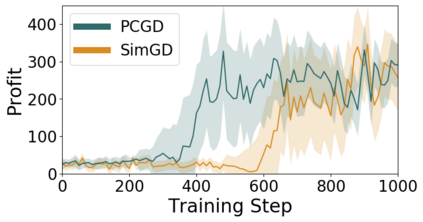
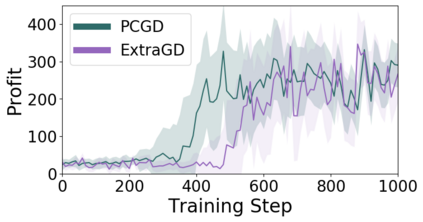
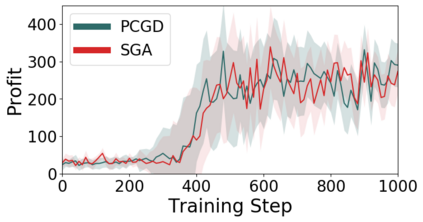
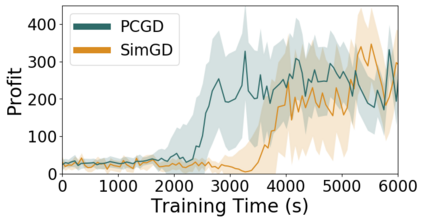
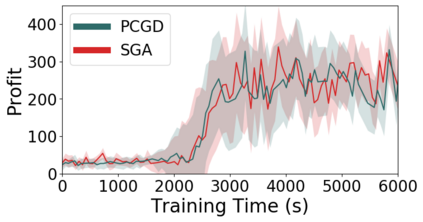
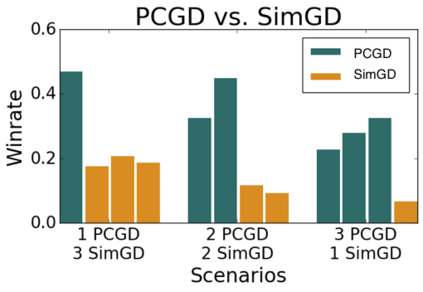
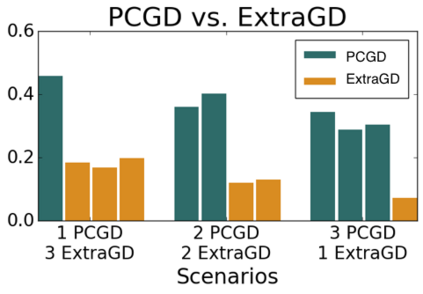
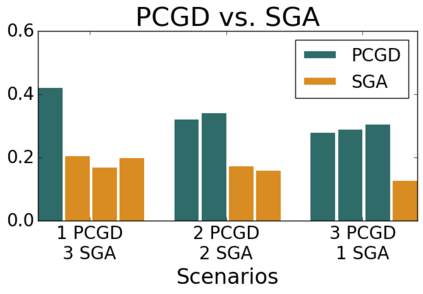
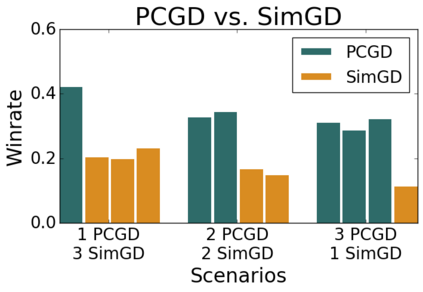
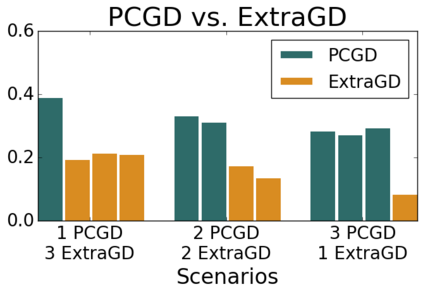
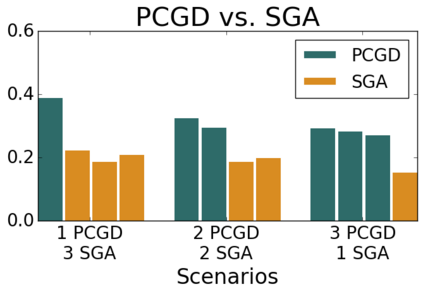
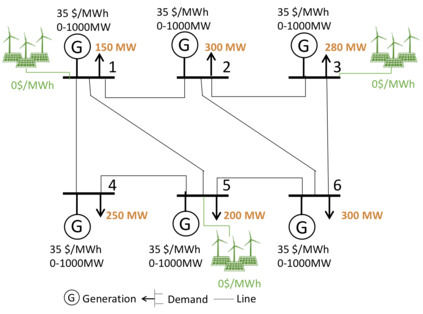
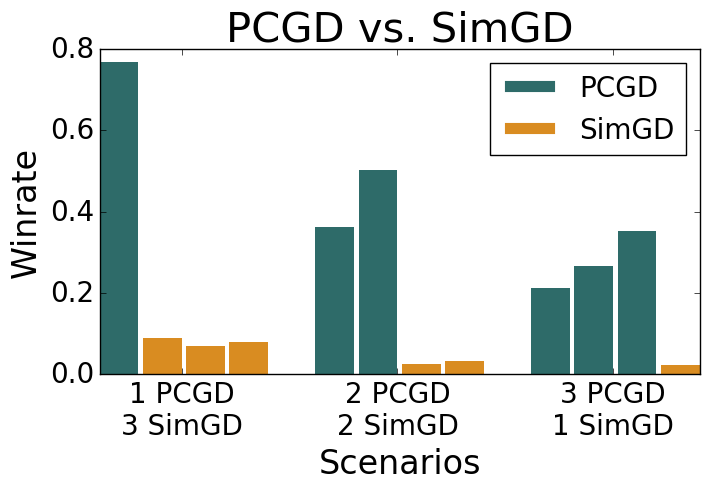
Many economic games and machine learning approaches can be cast as competitive optimization problems where multiple agents are minimizing their respective objective function, which depends on all agents' actions. While gradient descent is a reliable basic workhorse for single-agent optimization, it often leads to oscillation in competitive optimization. In this work we propose polymatrix competitive gradient descent (PCGD) as a method for solving general sum competitive optimization involving arbitrary numbers of agents. The updates of our method are obtained as the Nash equilibria of a local polymatrix approximation with a quadratic regularization, and can be computed efficiently by solving a linear system of equations. We prove local convergence of PCGD to stable fixed points for $n$-player general-sum games, and show that it does not require adapting the step size to the strength of the player-interactions. We use PCGD to optimize policies in multi-agent reinforcement learning and demonstrate its advantages in Snake, Markov soccer and an electricity market game. Agents trained by PCGD outperform agents trained with simultaneous gradient descent, symplectic gradient adjustment, and extragradient in Snake and Markov soccer games and on the electricity market game, PCGD trains faster than both simultaneous gradient descent and the extragradient method.
翻译:许多经济游戏和机器学习方法可被看成是竞争性优化问题,在这种情况下,多种代理机构正在最大限度地降低其各自的客观功能,这取决于所有代理机构的行动。虽然梯度下降是单一代理机构优化的可靠基本工作马匹,但往往会在竞争优化中导致振动。在这项工作中,我们提议多式矩阵竞争性梯度下降(PCGD),作为解决涉及任意数个代理机构的一般性和竞争性优化的方法。我们的方法的更新是以四面形正规化的当地多面体近似的纳什平衡方式获得的,并且可以通过解决直线方程系统来有效计算。我们证明PCGD与美元玩家普通和普通游戏的稳定固定点在当地趋同,并表明它不需要根据玩家互动行动的力量调整步数。我们使用PCGD来优化多面强化学习的政策,并展示其在蛇、Markov足球和电力市场游戏中的优势。由PCGDD外形剂培训的代理机构通过同时梯度下降、随机梯度调整以及蛇与Markov足球运动的超高位化方法培训。