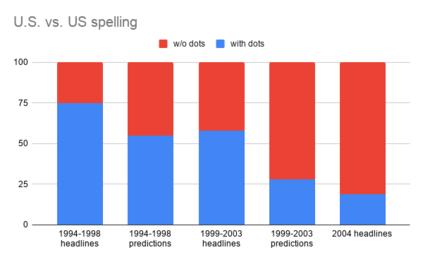
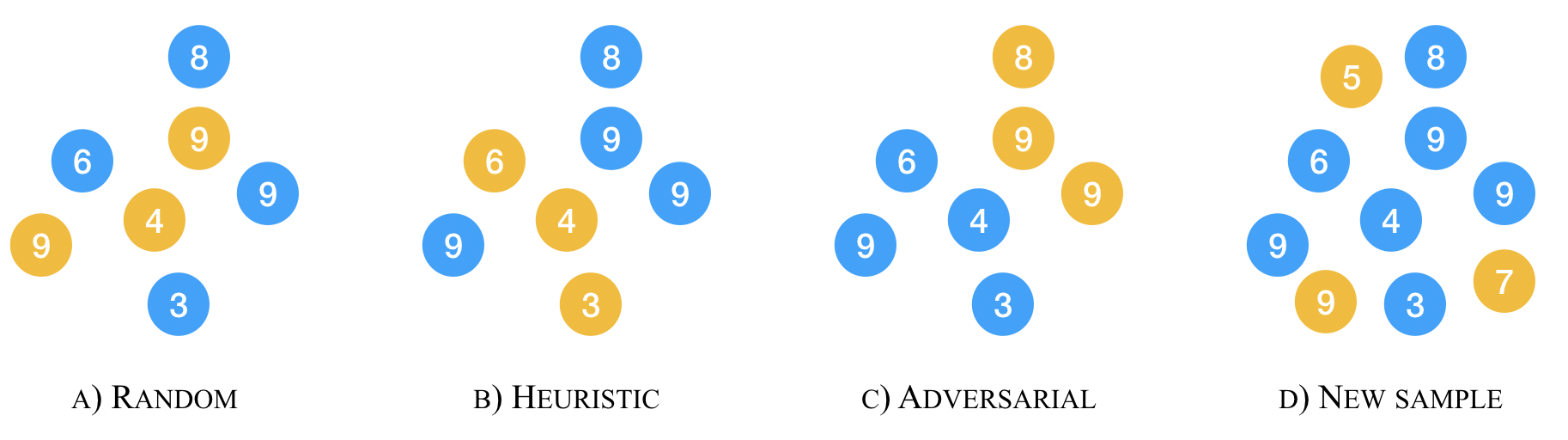
Gorman and Bedrick (2019) argued for using random splits rather than standard splits in NLP experiments. We argue that random splits, like standard splits, lead to overly optimistic performance estimates. We can also split data in biased or adversarial ways, e.g., training on short sentences and evaluating on long ones. Biased sampling has been used in domain adaptation to simulate real-world drift; this is known as the covariate shift assumption. In NLP, however, even worst-case splits, maximizing bias, often under-estimate the error observed on new samples of in-domain data, i.e., the data that models should minimally generalize to at test time. This invalidates the covariate shift assumption. Instead of using multiple random splits, future benchmarks should ideally include multiple, independent test sets instead; if infeasible, we argue that multiple biased splits leads to more realistic performance estimates than multiple random splits.
翻译:Gorman和Bedrick (2019年) 主张在 NLP 实验中使用随机分解而不是标准分解。 我们争辩说, 随机分解, 如标准分解, 会导致过度乐观的性能估计。 我们还可以偏颇或对称的方式分割数据, 比如, 短刑期培训和长刑期评估。 在模拟真实世界漂移的域适应中, 误差抽样被使用; 这被称为共变转换假设 。 但是, 在 NLP 实验中, 即使是最坏的分解, 最大偏差, 也往往低估新样本中观察到的误差, 即模型在测试时应尽量笼统化的数据。 这否定了共变转换的假设。 未来基准应该包括多个独立的测试组, 而不是多位随机分解; 如果不可行, 我们则认为, 多重偏差导致比多位随机拆分解更现实的性性性的工作估计。