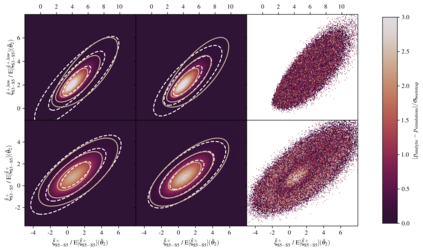
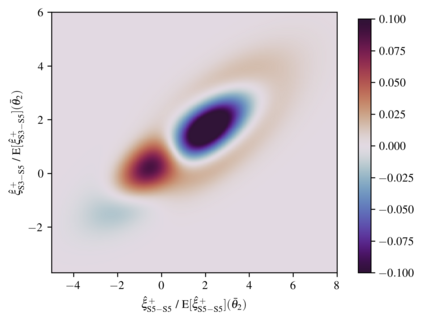
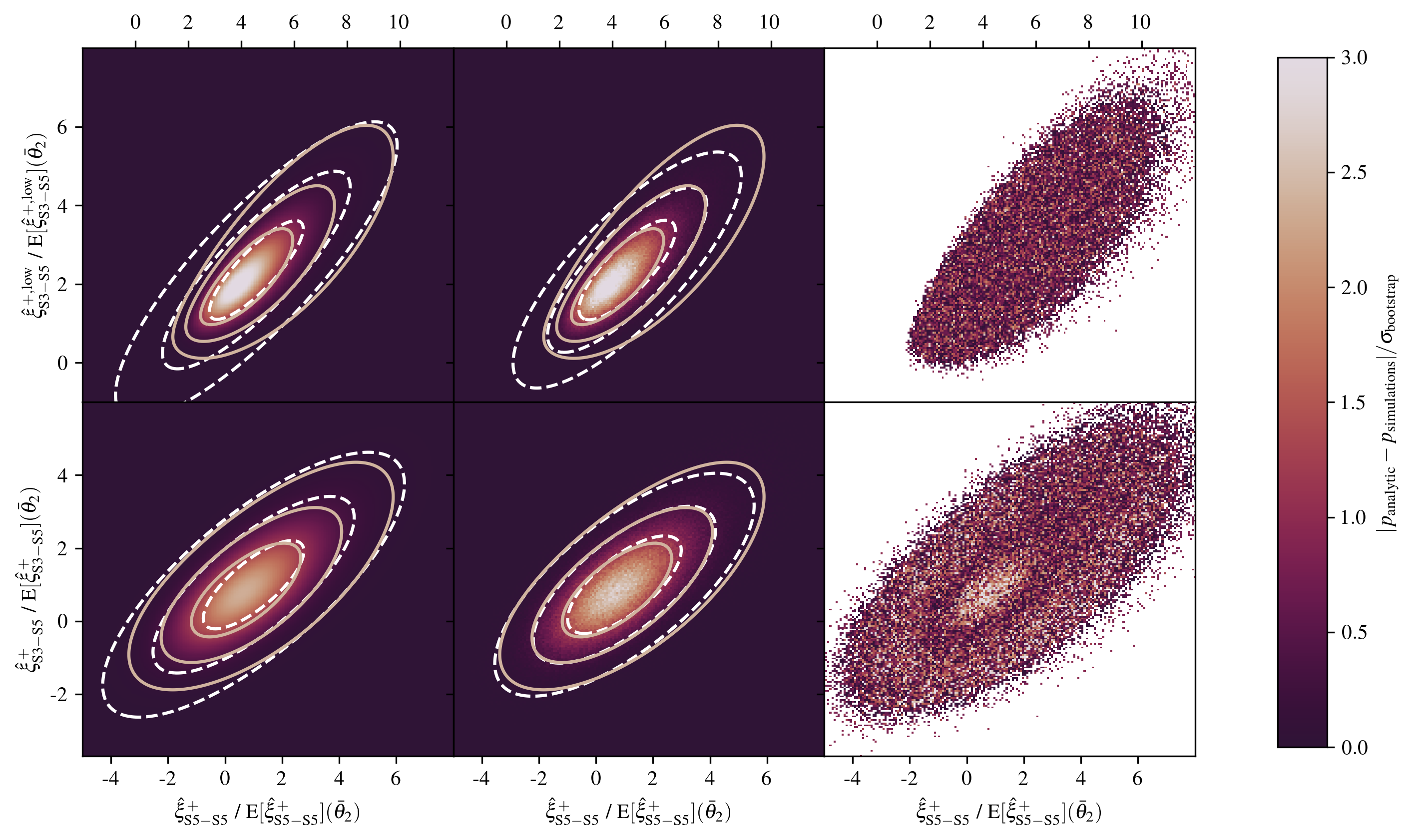
We present exact non-Gaussian joint likelihoods for auto- and cross-correlation functions on arbitrarily masked spherical Gaussian random fields. Our considerations apply to spin-0 as well as spin-2 fields but are demonstrated here for the spin-2 weak-lensing correlation function. We motivate that this likelihood cannot be Gaussian and show how it can nevertheless be calculated exactly for any mask geometry and on a curved sky, as well as jointly for different angular-separation bins and redshift-bin combinations. Splitting our calculation into a large- and small-scale part, we apply a computationally efficient approximation for the small scales that does not alter the overall non-Gaussian likelihood shape. To compare our exact likelihoods to correlation-function sampling distributions, we simulated a large number of weak-lensing maps, including shape noise, and find excellent agreement for one-dimensional as well as two-dimensional distributions. Furthermore, we compare the exact likelihood to the widely employed Gaussian likelihood and find significant levels of skewness at angular separations $\gtrsim 1^{\circ}$ such that the mode of the exact distributions is shifted away from the mean towards lower values of the correlation function. We find that the assumption of a Gaussian random field for the weak-lensing field is well valid at these angular separations. Considering the skewness of the non-Gaussian likelihood, we evaluate its impact on the posterior constraints on $S_8$. On a simplified weak-lensing-survey setup with an area of $10 \ 000 \ \mathrm{deg}^2$, we find that the posterior mean of $S_8$ is up to $2\%$ higher when using the non-Gaussian likelihood, a shift comparable to the precision of current stage-III surveys.
翻译:暂无翻译