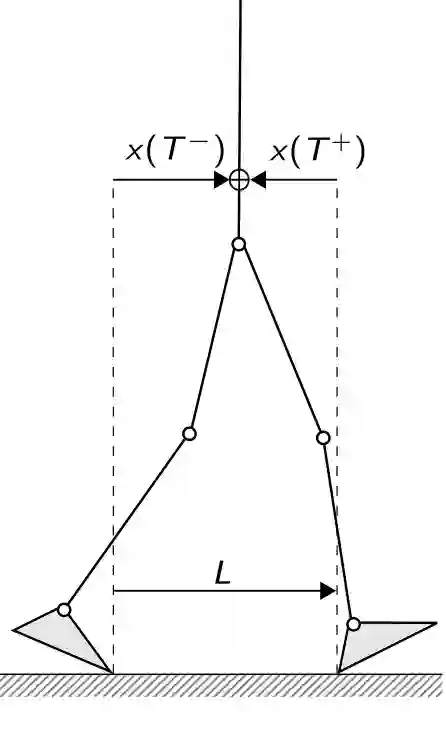
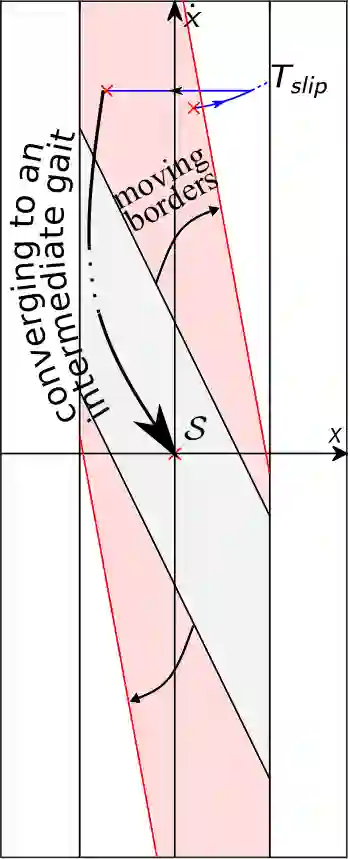
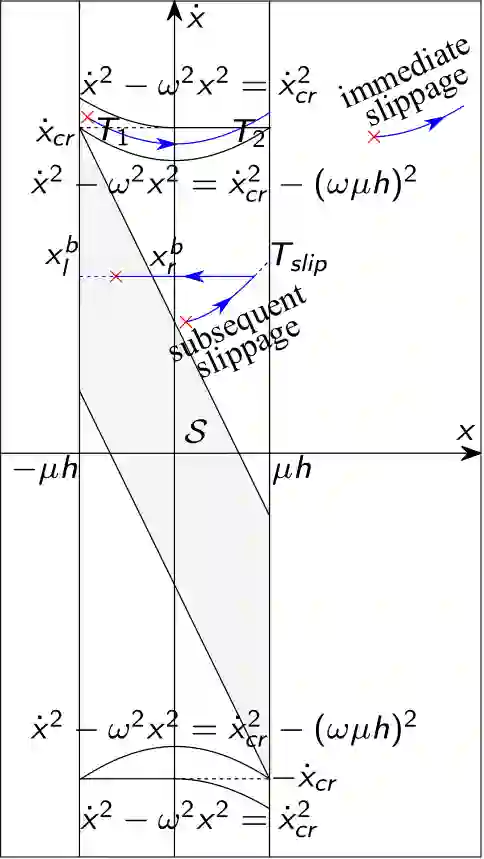
Despite extensive studies on motion stabilization of bipeds, they still suffer from the lack of disturbance coping capability on slippery surfaces. In this paper, a novel controller for stabilizing a bipedal motion in its sagittal plane is developed with regard to the surface friction limitations. By taking into account the physical limitation of the surface in the stabilization trend, a more advanced level of reliability is achieved that provides higher functionalities such as push recovery on low-friction surfaces and prevents the stabilizer from overreacting. The discrete event-based strategy consists of modifying the step length and time period at the beginning of each footstep in order to reestablish stability necessary conditions while taking into account the surface friction limitation as a constraint to prevent slippage. Adjusting footsteps to prevent slippage in confronting external disturbances is perceived as a novel strategy for keeping stability, quite similar to human reaction. The developed methodology consists of rough closed-form solutions utilizing elementary math operations for obtaining the control inputs, allowing to reach a balance between convergence and computational cost, which is quite suitable for real-time operations even with modest computational hardware. Several numerical simulations, including push recovery and switching between different gates on low-friction surfaces, are performed to demonstrate the effectiveness of the proposed controller. In correlation with human-gait experience, the results also reveal some physical aspects favoring stability and the fact of switching between gaits to reduce the risk of falling in confronting different conditions.
翻译:尽管对双胞胎运动稳定进行了广泛的研究,但是它们仍然缺乏在滑滑的表面的应对能力。在本文中,在表面摩擦限制方面,开发了稳定其两脚运动的新控制器,以稳定其表面两脚运动。考虑到稳定趋势中表面的物理限制,可以实现更先进的可靠性,提供更高的功能,如在低运动表面推动恢复,防止稳定。以事件为基础的战略包括在每步开始的时候修改步长和时段,以重建必要的稳定条件,同时将表面摩擦限制作为防止滑坡的制约因素。调整脚步以防止应对外部动乱的滑坡,被视为一种保持稳定的新战略,与人类反应非常相似。开发的方法包括粗的封闭式解决方案,利用基本数学操作获得控制投入,从而在趋同和计算成本之间取得平衡,即使计算硬件不高,也非常适合实时操作。一些数字模拟,包括推动恢复和转变不同门之间对面的定位,同时展示了在低稳定面表面变化结果上的拟议对冲结果。