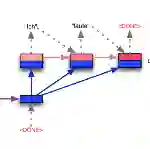
In this paper, we show that structures similar to self-attention are natural to learn many sequence-to-sequence problems from the perspective of symmetry. Inspired by language processing applications, we study the orthogonal equivariance of seq2seq functions with knowledge, which are functions taking two inputs -- an input sequence and a ``knowledge'' -- and outputting another sequence. The knowledge consists of a set of vectors in the same embedding space as the input sequence, containing the information of the language used to process the input sequence. We show that orthogonal equivariance in the embedding space is natural for seq2seq functions with knowledge, and under such equivariance the function must take the form close to the self-attention. This shows that network structures similar to self-attention are the right structures to represent the target function of many seq2seq problems. The representation can be further refined if a ``finite information principle'' is considered, or a permutation equivariance holds for the elements of the input sequence.
翻译:在本文中, 我们显示与自我注意相似的结构自然会从对称的角度来学习许多序列到序列的问题。 在语言处理应用程序的启发下, 我们研究具有知识的后继2当量函数的正对等性, 这些函数需要两种输入 -- -- 一个输入序列和一个“ 知识” -- -- 并输出另一个序列。 知识由输入序列的同一嵌入空间的一组矢量组成, 包含处理输入序列所用语言的信息。 我们显示, 嵌入空间的正对等性对于具有知识的后继2当量函数是自然的, 在这种等同性情况下, 函数必须采取接近自省的形式。 这显示, 与自我注意相似的网络结构是代表许多后继2当量问题目标功能的正确结构。 如果考虑“ 确定信息原则”, 或者输入序列要素的变异性, 代表可以进一步完善。