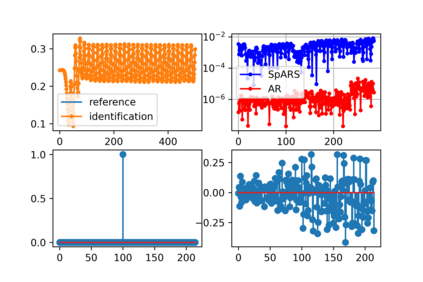
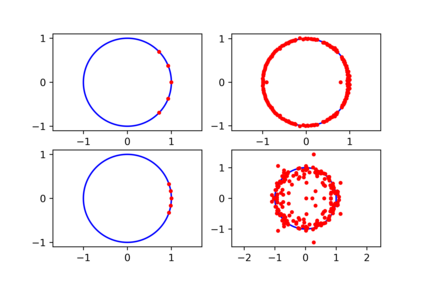
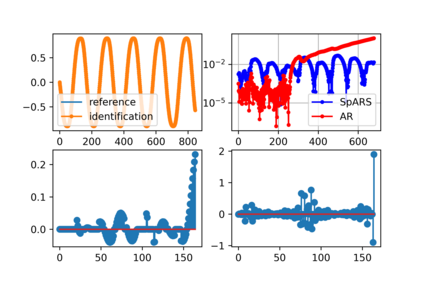
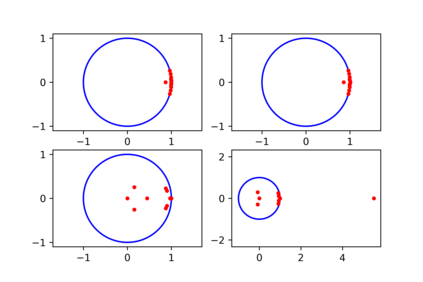
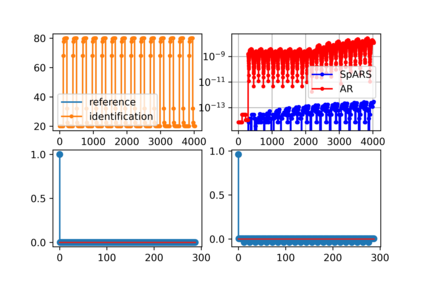
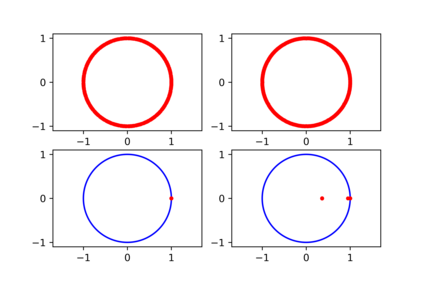
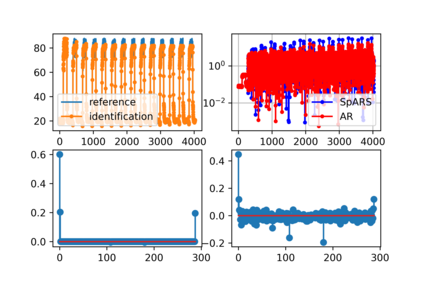
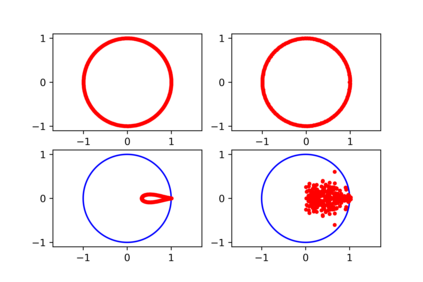
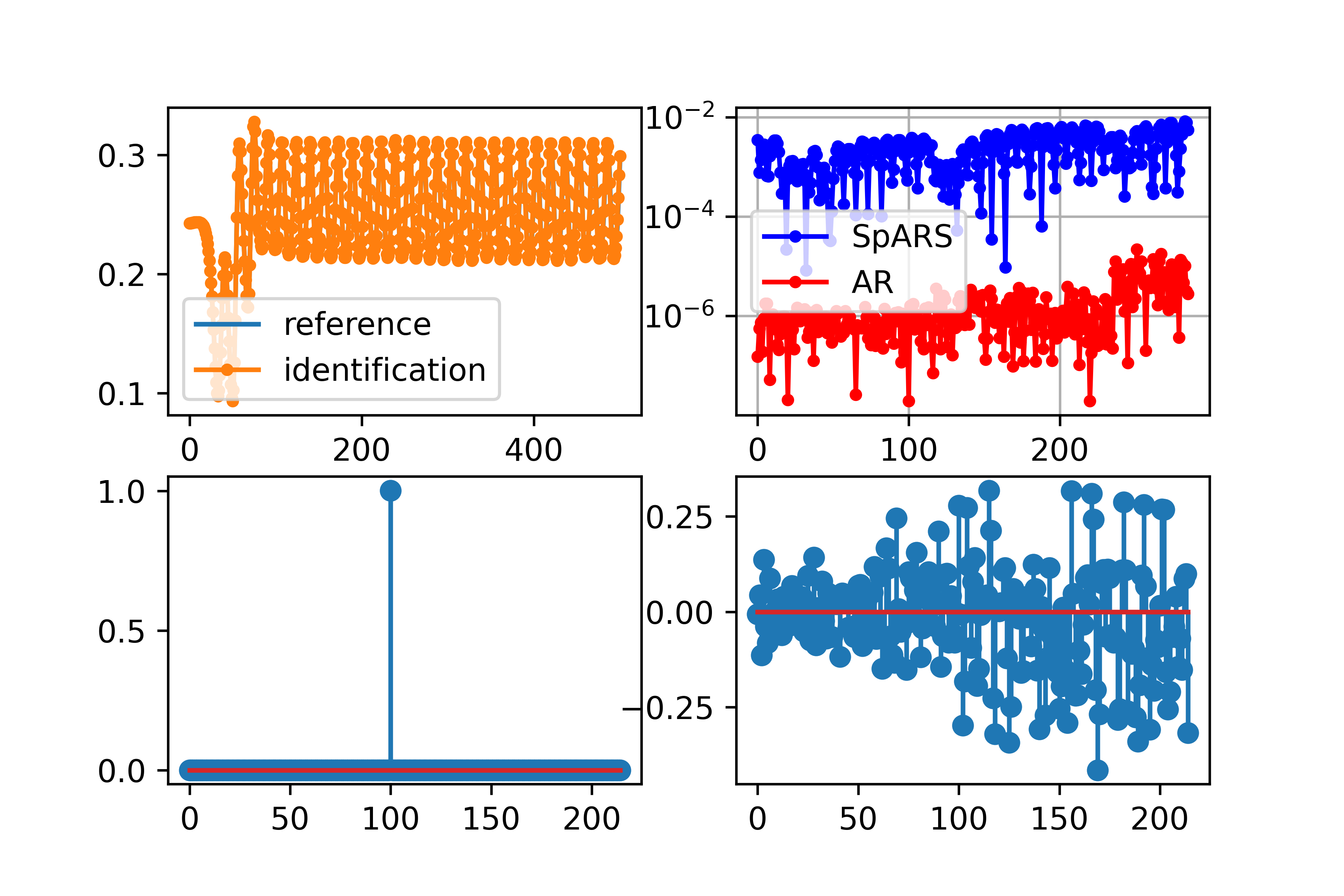
Some elements of the theory and algorithmics corresponding to the computation of semilinear sparse models for discrete-time signals are presented. In this study, we will focus on approximately eventually periodic discrete-time signals, that is, signals that can exhibit an aperiodic behavior for an initial amount of time, and then become approximately periodic afterwards. The semilinear models considered in this study are obtained by combining sparse representation methods, linear autoregressive models and GRU neural network models, initially fitting each block model independently using some reference data corresponding to some signal under consideration, and then fitting some mixing parameters that are used to obtain a signal model consisting of a linear combination of the previously fitted blocks using the aforementioned reference data, computing sparse representations of some of the matrix parameters of the resulting model along the process. Some prototypical computational implementations are presented as well.
翻译:介绍了与计算离散时间信号半线性分散模型相对应的一些理论和算法要素。在本研究中,我们将侧重于大约最终的周期性离散时间信号,即能够显示初步时间周期性行为的信号,然后在最初一段时间内成为大约定期性的信号。本研究中考虑的半线性模型是通过结合稀释代表法、线性自动递减模型和GRU神经网络模型获得的,最初利用与审议中的某种信号相对应的一些参考数据独立地对每个区块模型进行安装,然后安装一些混合参数,用于获取信号模型,其中包括利用上述参考数据将以前安装的区块线性组合成一个线性组合,在过程中计算由此产生的模型的一些矩阵参数的稀少情况。还介绍了一些原型计算执行情况。