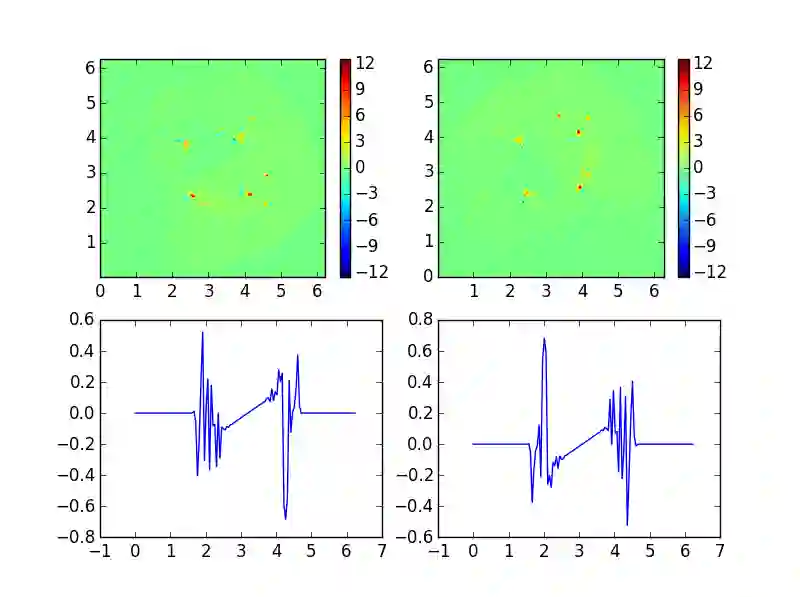
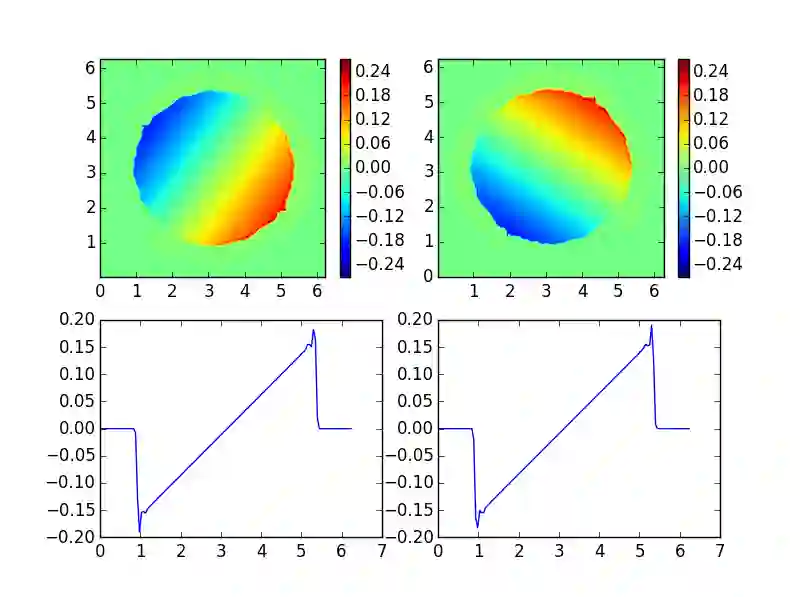
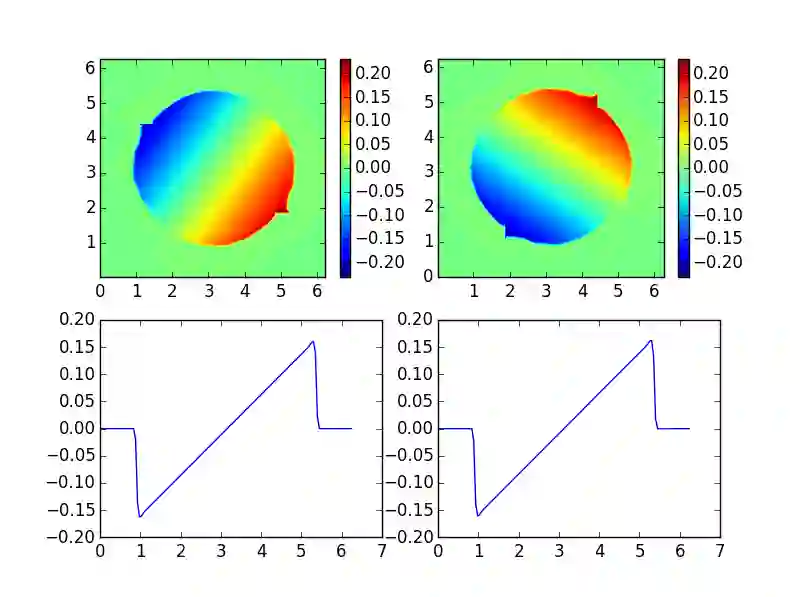
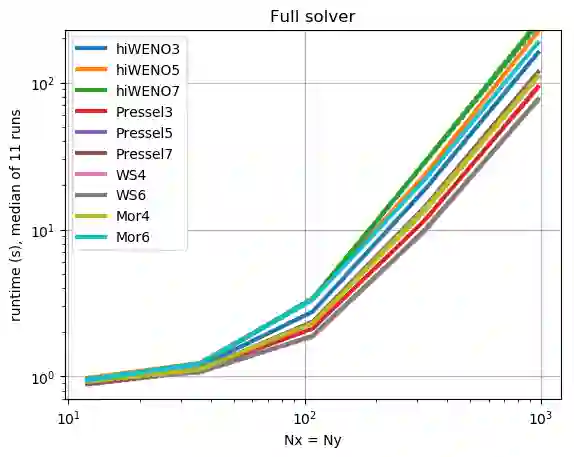
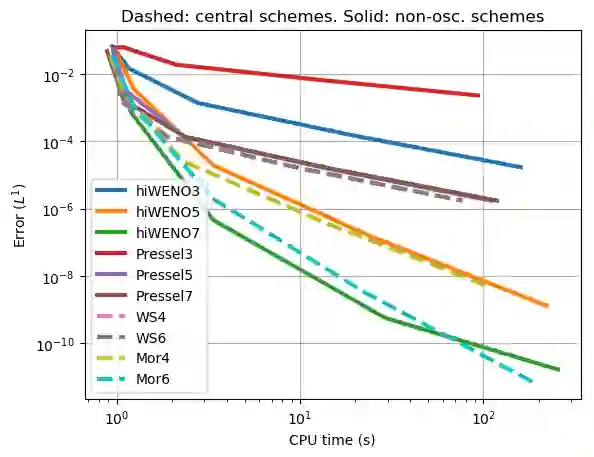
We propose a WENO finite difference scheme to approximate anelastic flows, and scalars advected by them, on staggered grids. In contrast to existing WENO schemes on staggered grids, the proposed scheme is designed to be arbitrarily high-order accurate as it judiciously combines ENO interpolations of velocities with WENO reconstructions of spatial derivatives. A set of numerical experiments are presented to demonstrate the increase in accuracy and robustness with the proposed scheme, when compared to existing WENO schemes and state-of-the-art central finite difference schemes.
翻译:我们提出了一个WENO有限差别计划,以在交错格网格上近似弹性流和由它们支撑的天平。 与现有的WENO网格错开办法相比,拟议办法的设计是任意性高端准确,因为它明智地将ENO速度的内插和WENO空间衍生物的重建结合起来。 提出了一系列数字实验,以表明与现有的WENO方案和最新中央有限差别计划相比,拟议办法的准确性和稳健性有所提高。