How many perturbations break this model? Evaluating robustness beyond adversarial accuracy

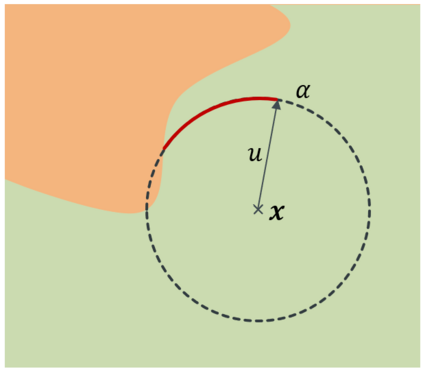
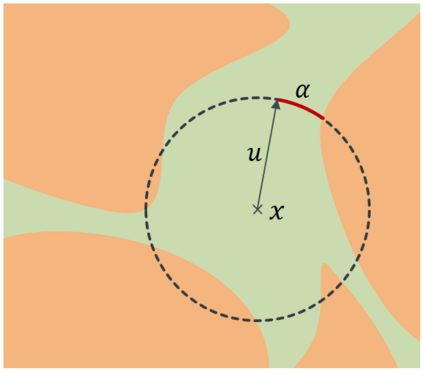
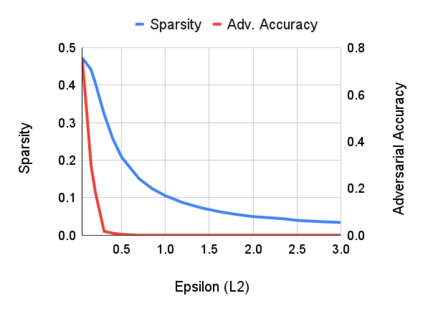
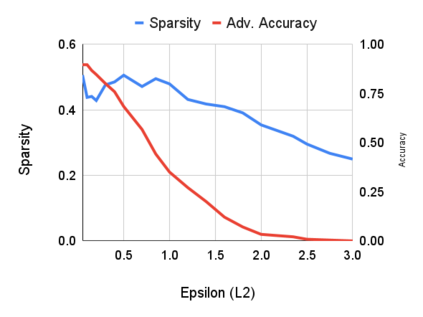
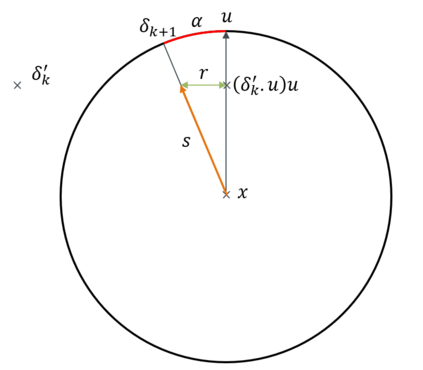
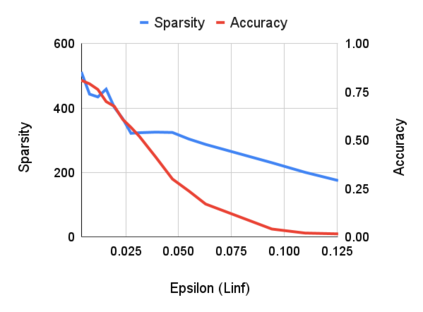
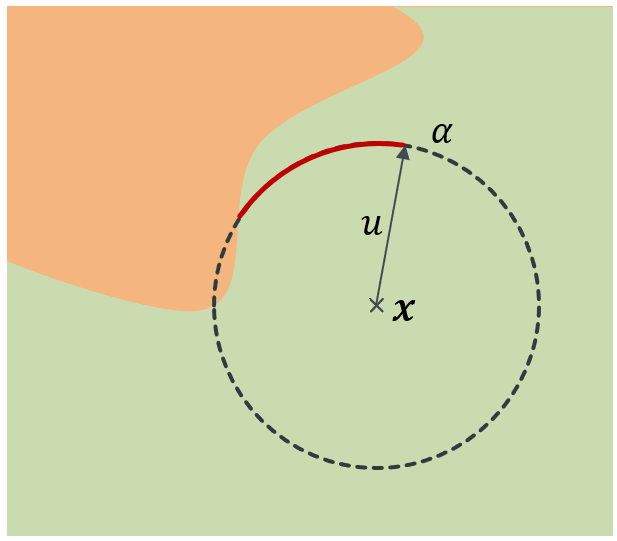
Robustness to adversarial attack is typically evaluated with adversarial accuracy. This metric quantifies the number of points for which, given a threat model, successful adversarial perturbations cannot be found. While essential, this metric does not capture all aspects of robustness and in particular leaves out the question of how many perturbations can be found for each point. In this work we introduce an alternative approach, adversarial sparsity, which quantifies how difficult it is to find a successful perturbation given both an input point and a constraint on the direction of the perturbation. This constraint may be angular (L2 perturbations), or based on the number of pixels (Linf perturbations). We show that sparsity provides valuable insight on neural networks in multiple ways. analyzing the sparsity of existing robust models illustrates important differences between them that accuracy analysis does not, and suggests approaches for improving their robustness. When applying broken defenses effective against weak attacks but not strong ones, sparsity can discriminate between the totally ineffective and the partially effective defenses. Finally, with sparsity we can measure increases in robustness that do not affect accuracy: we show for example that data augmentation can by itself increase adversarial robustness, without using adversarial training.