The optimal strong convergence rates of the truncated EM and logarithmic truncated EM methods for multi-dimensional nonlinear stochastic differential equations

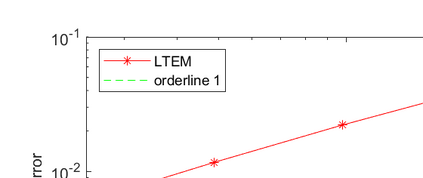
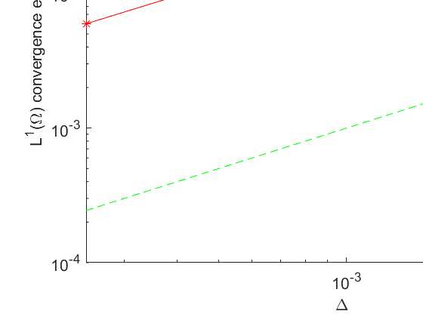
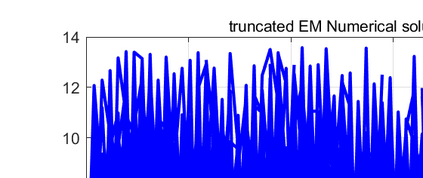
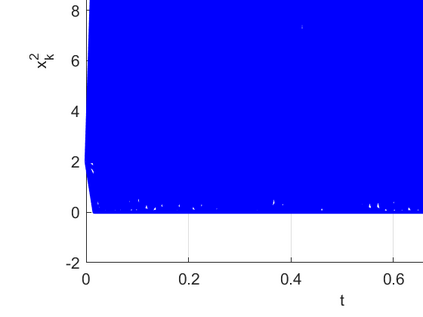
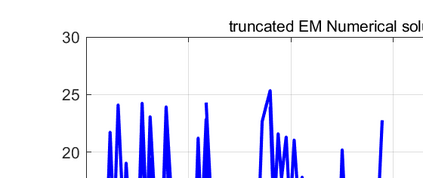
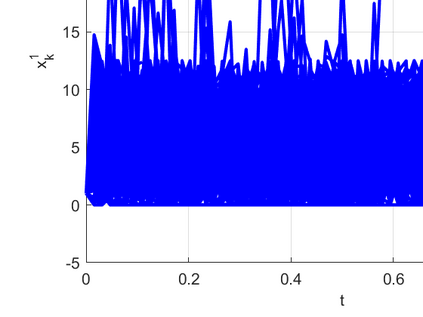
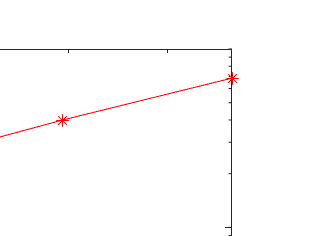
The truncated Euler--Maruyama (EM) method, developed by Mao (2015), is used to solve multi-dimensional nonlinear stochastic differential equations (SDEs). However, its convergence rate is suboptimal due to an unnecessary infinitesimal factor. The primary goal of this paper is to demonstrate the optimal convergence of the truncated EM method without infinitesimal factors. Besides, the logarithmic truncated EM method has not been studied in multi-dimensional cases, which is the other goal of this paper. We will show the optimal strong convergence order of the positivity-preserving logarithmic truncated EM method for solving multi-dimensional SDEs with positive solutions. Numerical examples are given to support our theoretical conclusions.