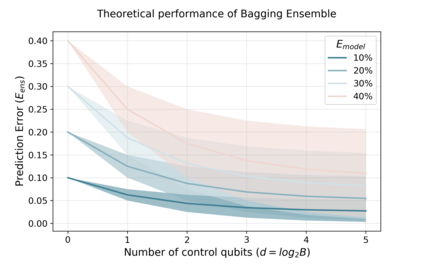
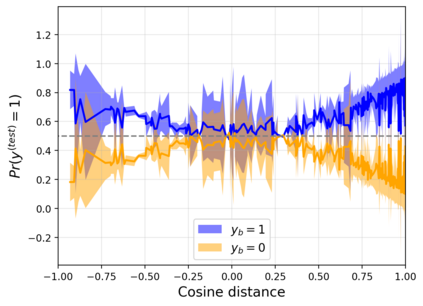
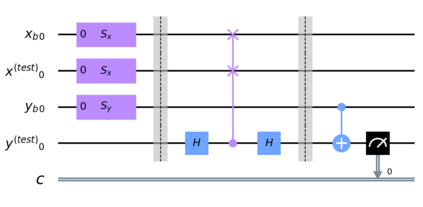
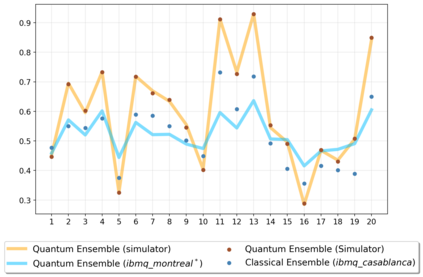
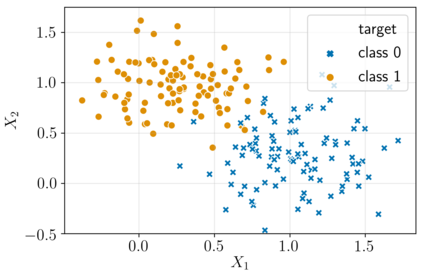
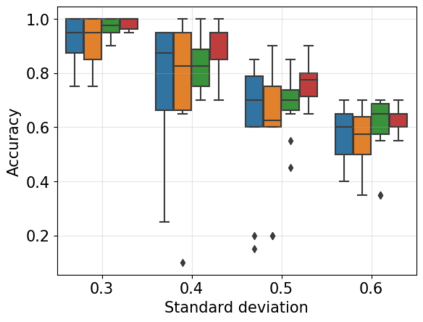
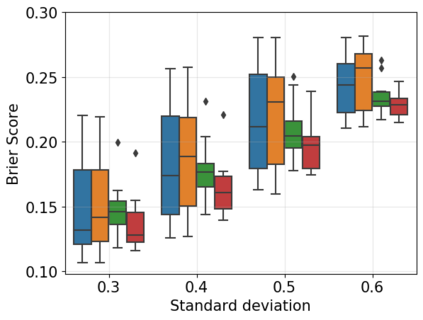
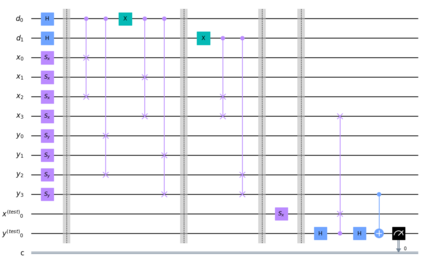
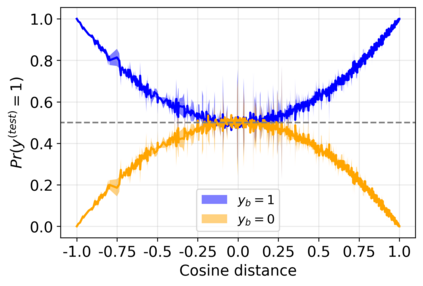
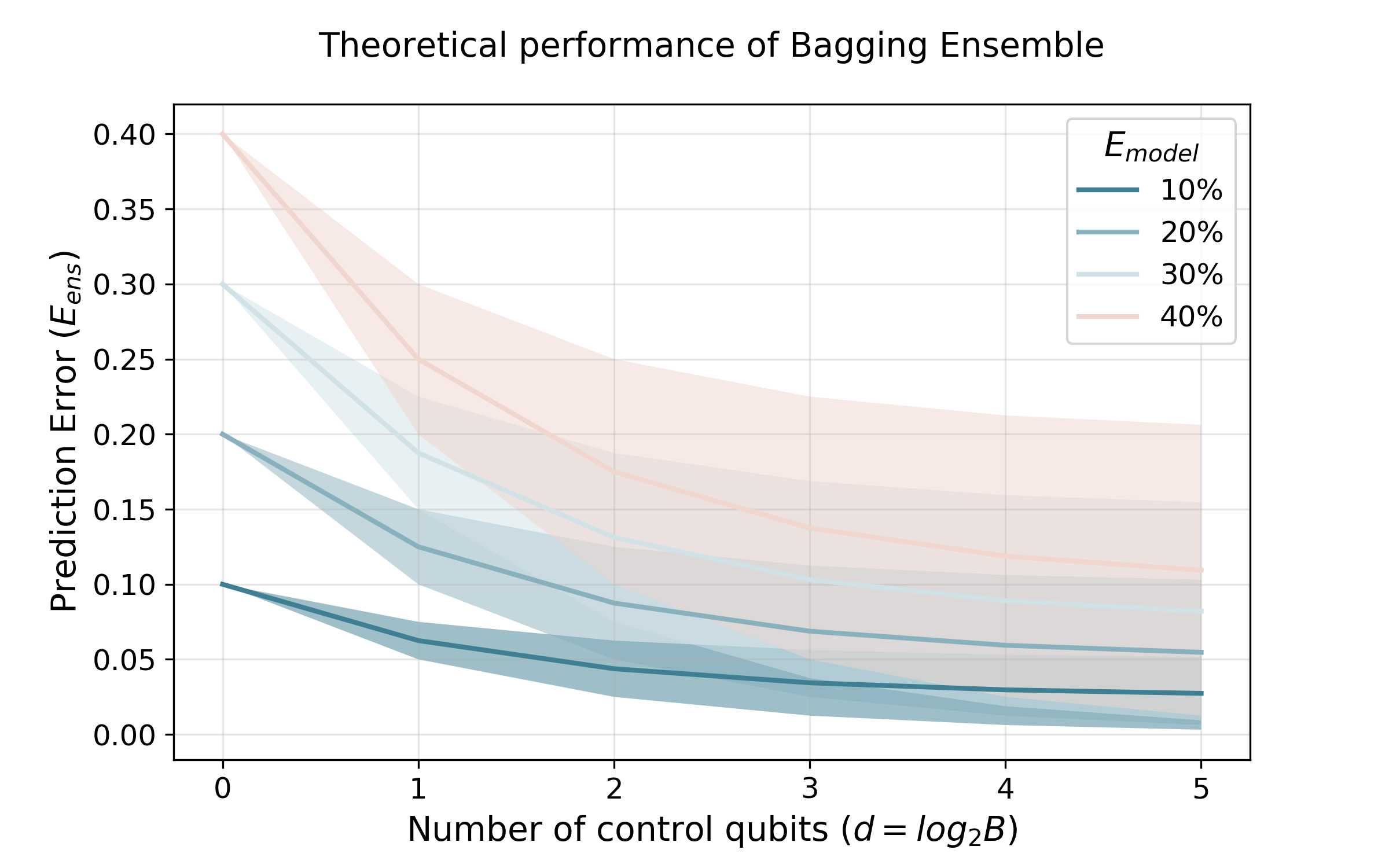
A powerful way to improve performance in machine learning is to construct an ensemble that combines the predictions of multiple models. Ensemble methods are often much more accurate and lower variance than the individual classifiers that make them up but have high requirements in terms of memory and computational time. In fact, a large number of alternative algorithms is usually adopted, each requiring to query all available data. We propose a new quantum algorithm that exploits quantum superposition, entanglement and interference to build an ensemble of classification models. Thanks to the generation of the several quantum trajectories in superposition, we obtain $B$ transformations of the quantum state which encodes the training set in only $log\left(B\right)$ operations. This implies exponential growth of the ensemble size while increasing linearly the depth of the correspondent circuit. Furthermore, when considering the overall cost of the algorithm, we show that the training of a single weak classifier impacts additively the overall time complexity rather than multiplicatively, as it usually happens in classical ensemble methods. We also present small-scale experiments on real-world datasets, defining a quantum version of the cosine classifier and using the IBM qiskit environment to show how the algorithms work.
翻译:提高机器学习性能的有力方法就是构建一个组合,将多种模型的预测结合起来。组合方法通常比单个分类师更准确、更低的差异,这些分类师组成这些方法,但在内存和计算时间方面要求很高。事实上,通常会采用大量替代算法,每个算法都需要查询所有可用数据。我们提出一种新的量子算法,利用量子叠加位置、缠绕和干扰来建立一系列分类模型。由于在超位中生成了几种量子轨迹,我们获得了数量状态的$B$转换,该变异编码了仅以$log\left(B\right)为单位设置的培训,但在记忆和计算时间和计算时间时间方面要求很高。此外,在考虑算算算算总成本时,我们展示了单一微分解器的训练会增加整个时间复杂性,而不是多倍增,因为它通常发生在典型的组合方法中。我们还在将仅以$loggleft(Bright)计算出仅以$$(Bright)计算出培训设置的量状态上进行了小尺度实验,同时定义了真实世界级的模型和Iqiral 数据环境。