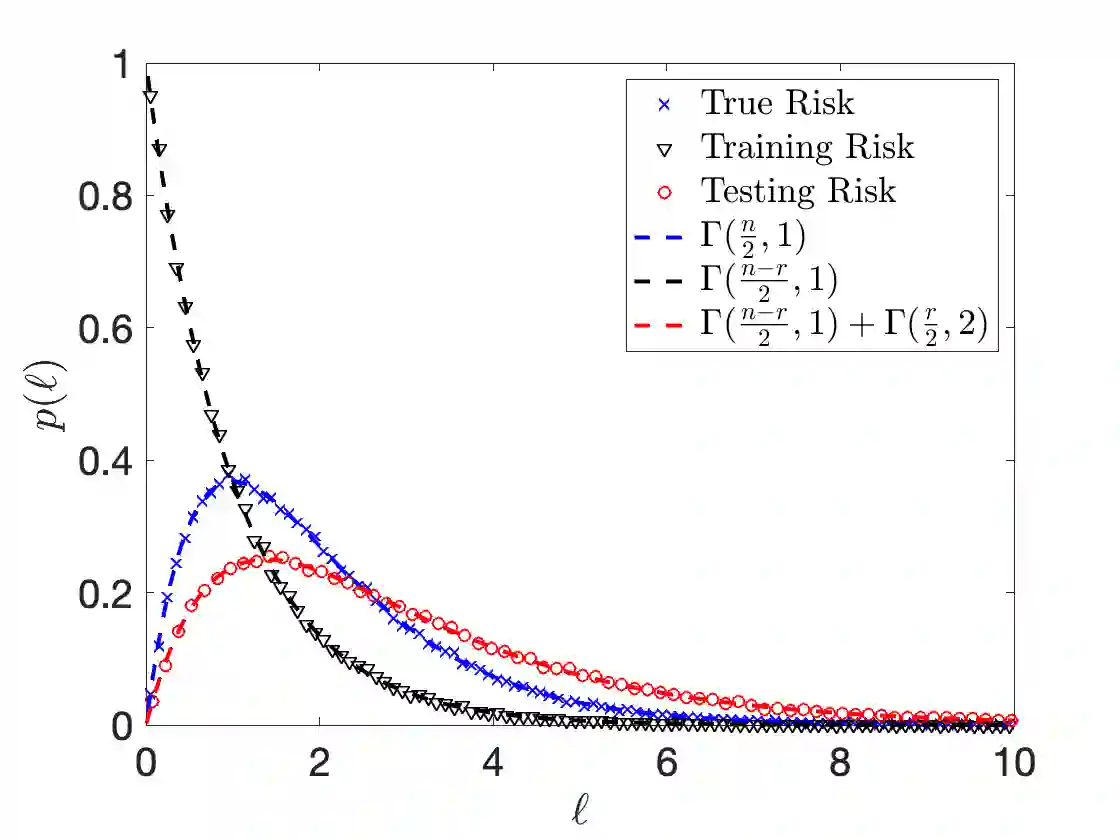
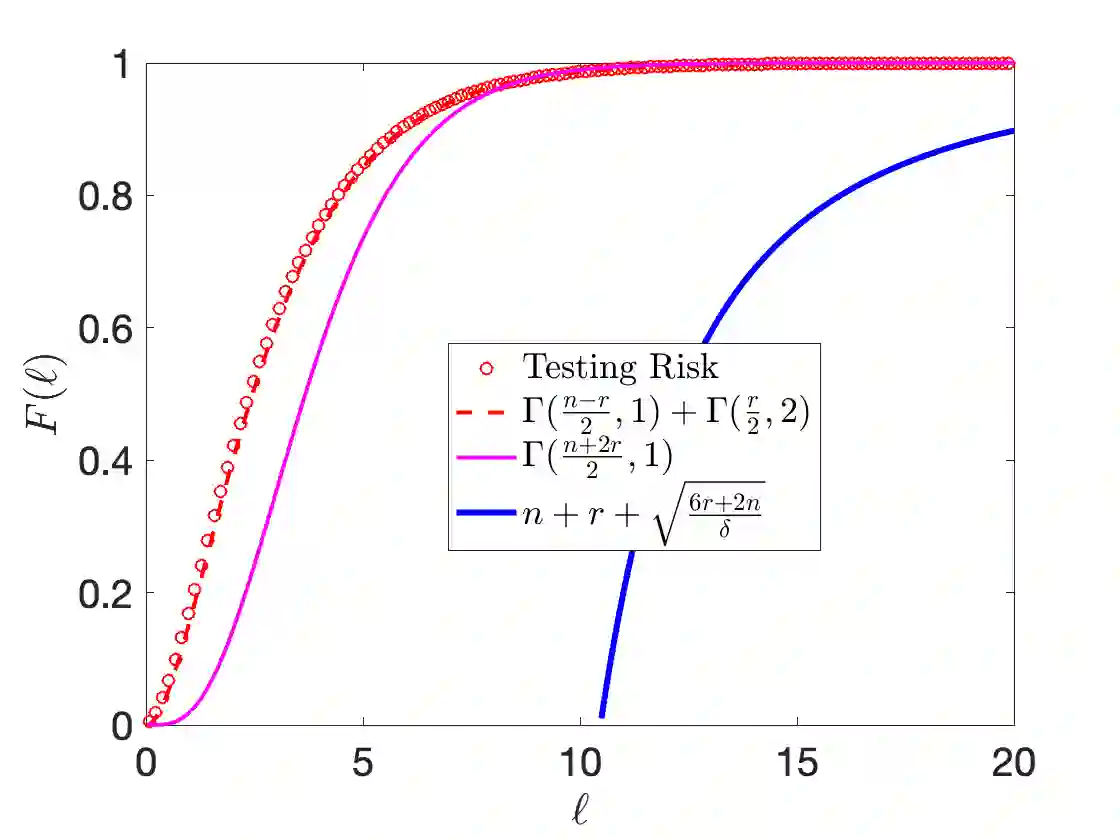
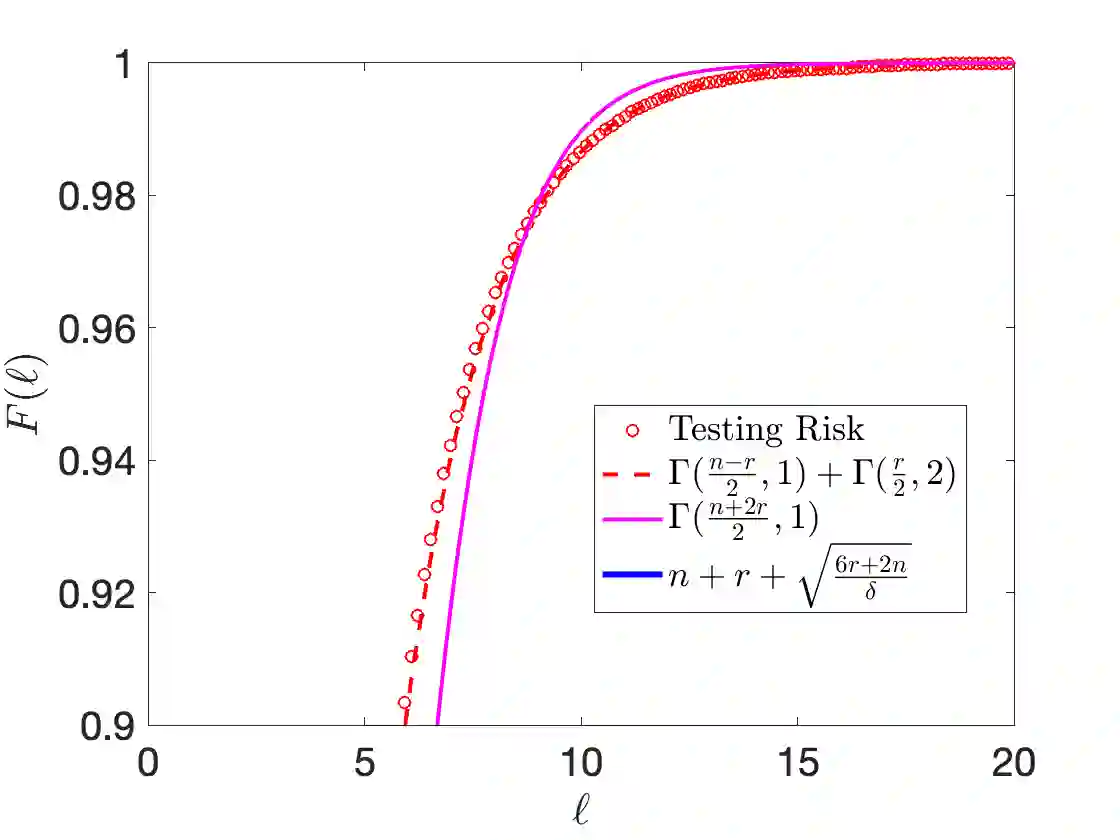
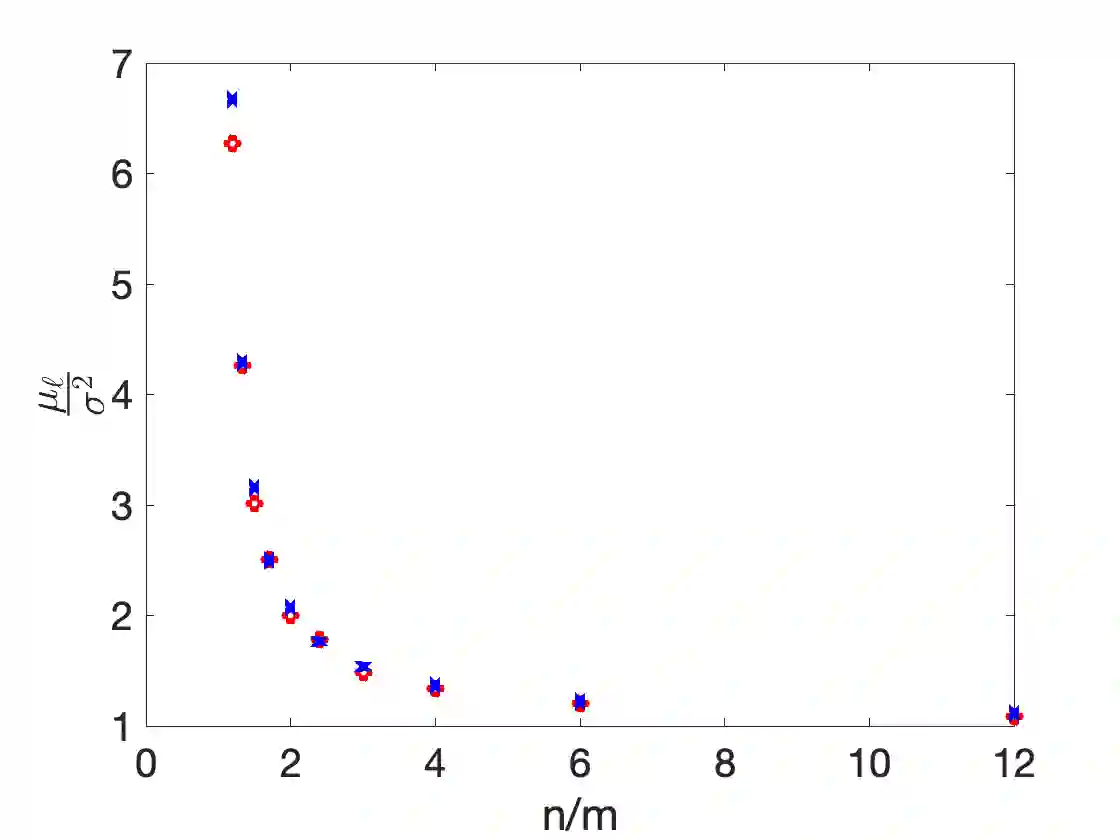
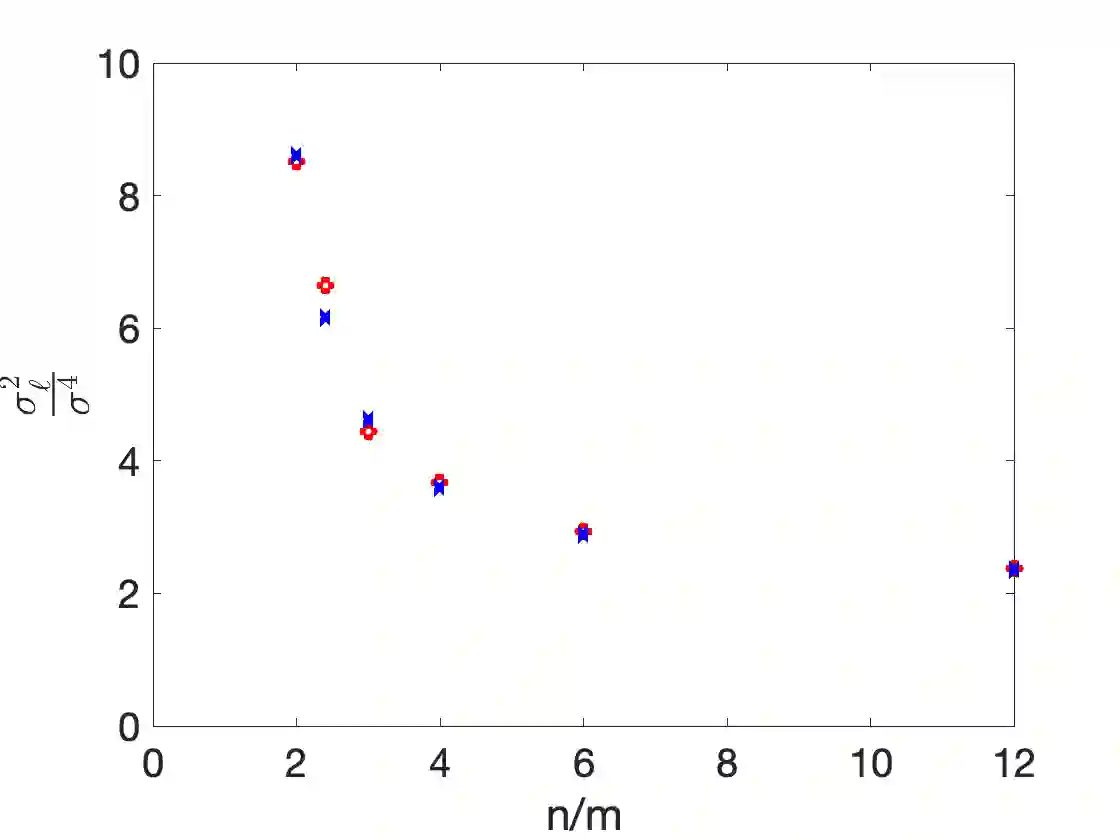
This note examines the behavior of generalization capabilities - as defined by out-of-sample mean squared error (MSE) - of Linear Gaussian (with a fixed design matrix) and Linear Least Squares regression. Particularly, we consider a well-specified model setting, i.e. we assume that there exists a `true' combination of model parameters within the chosen model form. While the statistical properties of Least Squares regression have been extensively studied over the past few decades - particularly with {\bf less restrictive problem statements} compared to the present work - this note targets bounds that are {\bf non-asymptotic and more quantitative} compared to the literature. Further, the analytical formulae for distributions and bounds (on the MSE) are directly compared to numerical experiments. Derivations are presented in a self-contained and pedagogical manner, in a way that a reader with a basic knowledge of probability and statistics can follow.
翻译:本说明审视了Linear Gaussian(具有固定设计矩阵)和Linear Oles最低广场回归(具有固定设计矩阵)的超模度平均正方差(MSE)定义的一般化能力行为。特别是,我们考虑了一个非常明确的模型设置,即我们假设在选定的模型形式内存在模型参数的“真实”组合。虽然过去几十年对最小方回归的统计特性进行了广泛研究,尤其是与目前的工作相比, & bf 较少限制性的问题说明 。但本说明的目标范围与文献相比是 $bf 非统计性,更具定量性。此外,分布和界限的分析公式(关于 MSE)与数字实验直接比较。 出处以自成一体和教学方式提出,使对概率和统计数据有基本了解的读者能够遵循的方式。