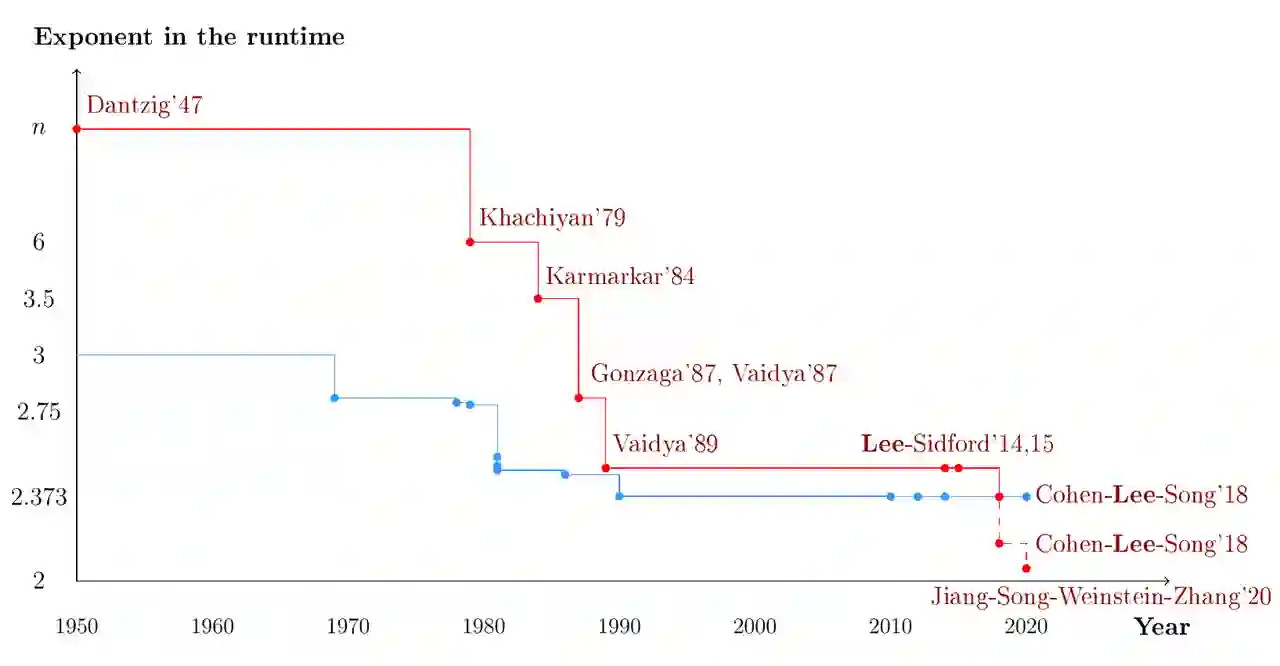
Algorithms for continuous optimization problems have a rich history of design and innovation over the past several decades, in which mathematical analysis of their convergence and complexity properties plays a central role. Besides their theoretical properties, optimization algorithms are interesting also for their practical usefulness as computational tools for solving real-world problems. There are often gaps between the practical performance of an algorithm and what can be proved about it. These two facets of the field -- the theoretical and the practical -- interact in fascinating ways, each driving innovation in the other. This work focuses on the development of algorithms in two areas -- linear programming and unconstrained minimization of smooth functions -- outlining major algorithm classes in each area along with their theoretical properties and practical performance, and highlighting how advances in theory and practice have influenced each other in these areas. In discussing theory, we focus mainly on non-asymptotic complexity, which are upper bounds on the amount of computation required by a given algorithm to find an approximate solution of problems in a given class.
翻译:连续优化问题的算法在过去几十年中经历了丰富的设计与创新历程,其中对其收敛性和复杂度性质的数学分析发挥着核心作用。除了理论特性外,优化算法作为解决实际问题的计算工具,其实际应用价值同样值得关注。算法的实际性能与其可证明的理论性质之间常存在差距。该领域的这两个方面——理论与实践——以引人入胜的方式相互影响,彼此推动着创新。本文聚焦于线性规划和平滑函数无约束最小化这两个领域的算法发展,概述了各领域的主要算法类别及其理论特性与实际表现,并重点阐述了这些领域中理论进展与实践应用如何相互促进。在理论探讨方面,我们主要关注非渐近复杂度,即给定算法在特定问题类中寻找近似解所需计算量的上界。