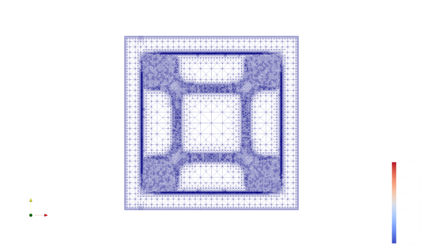
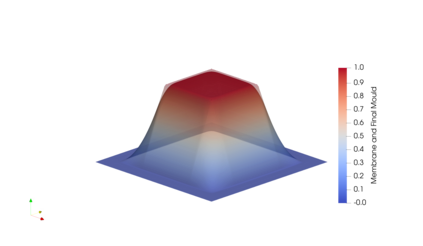
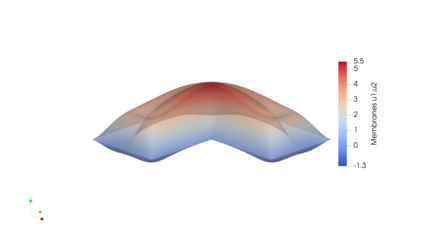
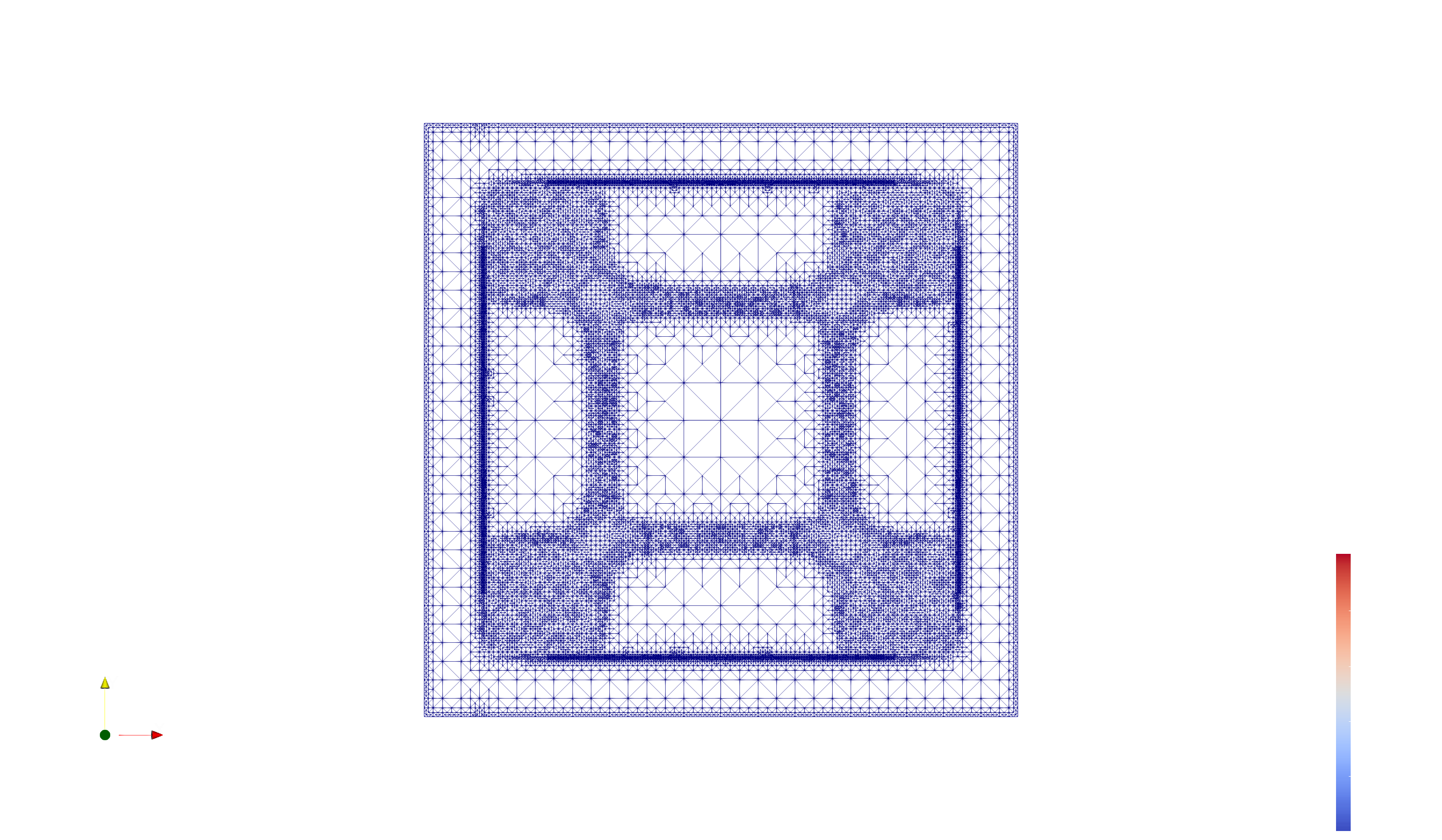
The present work aims at the application of finite element discretizations to a class of equilibrium problems involving moving constraints. Therefore, a Moreau--Yosida based regularization technique, controlled by a parameter, is discussed and, using a generalized $\Gamma$-convergence concept, a priori convergence results are derived. The latter technique is applied to the discretization of the regularized problems and is used to prove the convergence to the orginal equilibrium problem, when both -- regularization and discretization -- are imposed simultaneously. In addition, a primal-dual gap technique is used for the derivation of error estimators suitable for adaptive mesh refinement. A strategy for balancing between a refinement of the mesh and an update of the regularization parameter is established, too. The theoretical findings are illustrated for the obstacle problem as well as numerical experiments are performed for two quasi-variational inequalities with application to thermoforming and biomedicine, respectively.
翻译:目前的工作旨在对涉及移动制约的某一类均衡问题应用有限的元素分解,因此,讨论以参数为控制的基于Moreau-Yosida的正规化技术,并使用一个通用的美元-Gamma$-趋同概念,得出先验的趋同结果,后一种技术用于使正规化问题分解,并用来证明在同时同时实施 -- -- 正规化和离异 -- -- 时与边际平衡问题趋同。此外,还使用原始的双差法来得出适合适应网格改进的误差估计器。还制定了在网格精细与正规化参数更新之间取得平衡的战略,为障碍问题说明了理论结论,并分别对热化和生物医学应用的两种准变相不平等进行了数字实验。