Densely connected normalizing flows

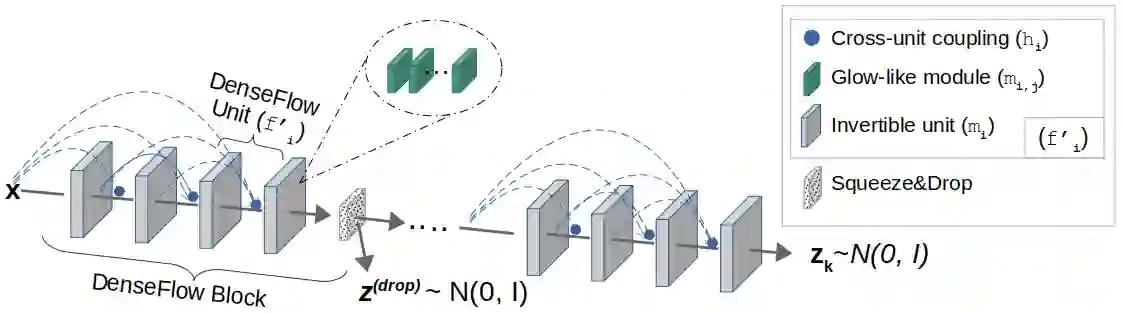
Normalizing flows are bijective mappings between inputs and latent representations with a fully factorized distribution. They are very attractive due to exact likelihood evaluation and efficient sampling. However, their effective capacity is often insufficient since the bijectivity constraint limits the model width. We address this issue by incrementally padding intermediate representations with noise. We precondition the noise in accordance with previous invertible units, which we describe as cross-unit coupling. Our invertible glow-like modules express intra-unit affine coupling as a fusion of a densely connected block and Nystr\"om self-attention. We refer to our architecture as DenseFlow since both cross-unit and intra-unit couplings rely on dense connectivity. Experiments show significant improvements due to the proposed contributions, and reveal state-of-the-art density estimation among all generative models under moderate computing budgets.