Learning common structures in a collection of networks. An application to food webs

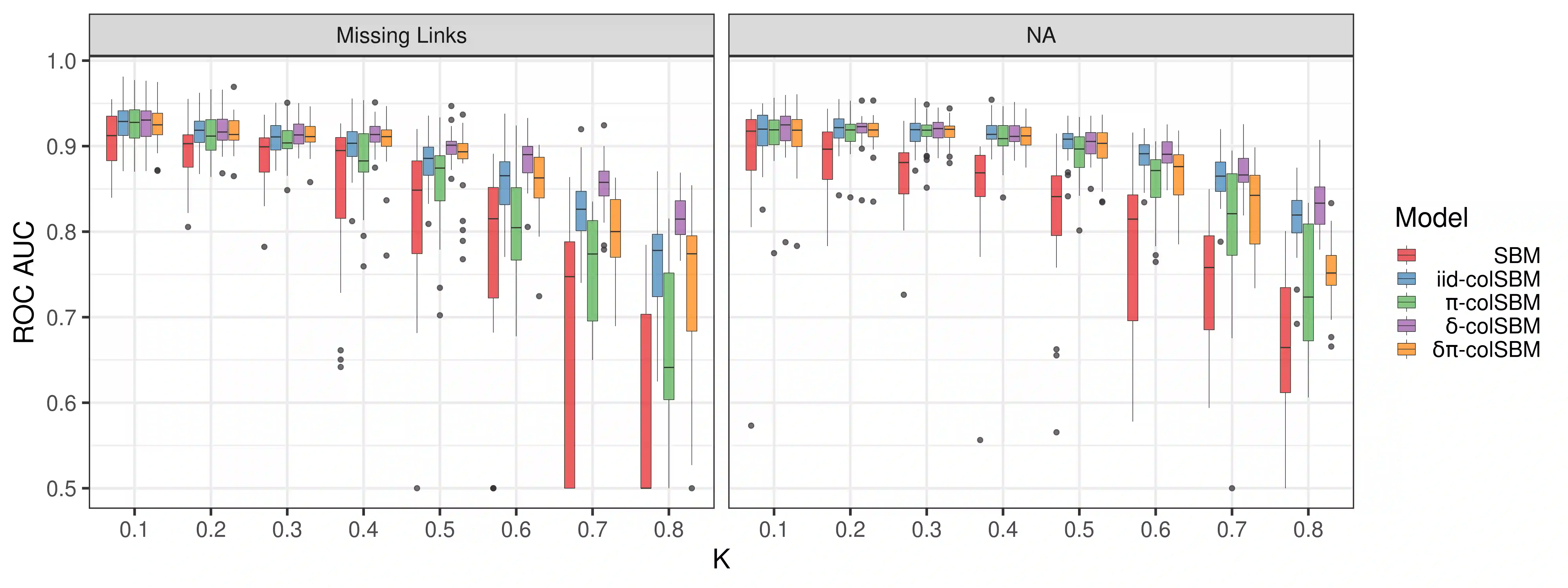
Let a collection of networks represent interactions within several (social or ecological) systems. Two main issues arise: identifying similarities between the topological structures of the networks or clustering the networks according to the similarities in their structures. We tackle these two questions with a probabilistic model based approach. We propose an extension of the Stochastic Block Model (SBM) adapted to the joint modeling of a collection of networks. The networks in the collection are assumed to be independent realizations of SBMs. The common connectivity structure is imposed through the equality of some parameters. The model parameters are estimated with a variational Expectation-Maximization (EM) algorithm. We derive an ad-hoc penalized likelihood criterion to select the number of blocks and to assess the adequacy of the consensus found between the structures of the different networks. This same criterion can also be used to cluster networks on the basis of their connectivity structure. It thus provides a partition of the collection into subsets of structurally homogeneous networks. The relevance of our proposition is assessed on two collections of ecological networks. First, an application to three stream food webs reveals the homogeneity of their structures and the correspondence between groups of species in different ecosystems playing equivalent ecological roles. Moreover, the joint analysis allows a finer analysis of the structure of smaller networks. Second, we cluster 67 food webs according to their connectivity structures and demonstrate that five mesoscale structures are sufficient to describe this collection.