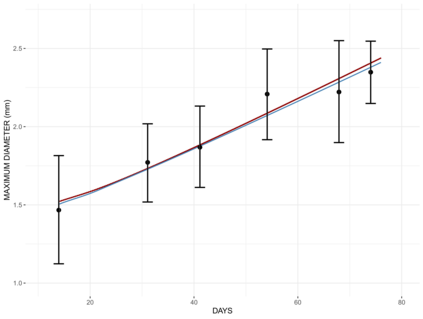
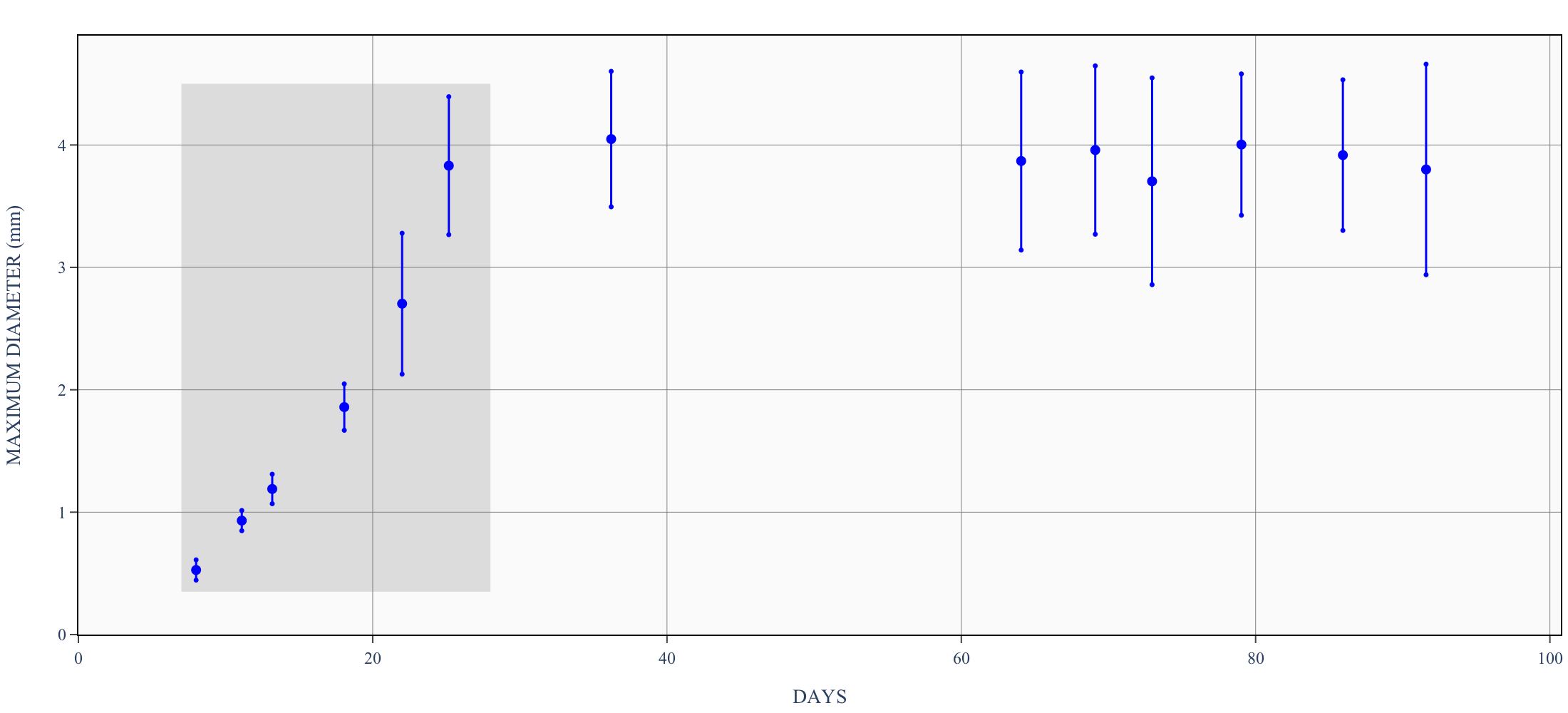
From a systems biology perspective the majority of cancer models, although interesting and providing a qualitative explanation of some problems, have a major disadvantage in that they usually miss a genuine connection with experimental data. Having this in mind, in this paper, we aim at contributing to the improvement of many cancer models which contain a proliferation term. To this end, we propose a new non-local model of cell proliferation. We select data which are suitable to perform a Bayesian inference for unknown parameters and we provide a discussion on the range of applicability of the model. Furthermore, we provide proof of the stability of a posteriori distributions in total variation norm which exploits the theory of spaces of measures equipped with the weighted flat norm. In a companion paper, we provide a detailed proof of the well-posedness of the problem and we investigate the convergence of the EBT algorithm applied to solve the equation.
翻译:从系统生物学的角度来看,大多数癌症模型虽然令人感兴趣,并且对一些问题提供了定性解释,但有一个重大不利之处,因为它们通常没有真正与实验数据联系起来。考虑到这一点,我们在本文件中的目标是帮助改进许多含有扩散术语的癌症模型。为此目的,我们提议一个新的非本地细胞扩散模型。我们选择了适合于对未知参数进行巴耶斯推论的数据,我们讨论了模型的适用范围。此外,我们提供了证据,证明利用带有加权平方标准的措施空间理论的完全变异规范的后端分布的稳定性。我们在一个配套文件中,我们详细证明了问题的准确性,并调查了用于解决等式的EBT算法的趋同性。