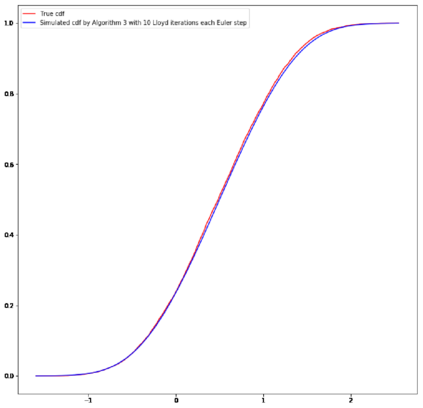
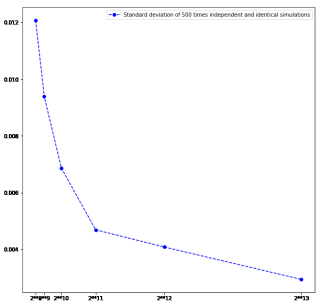
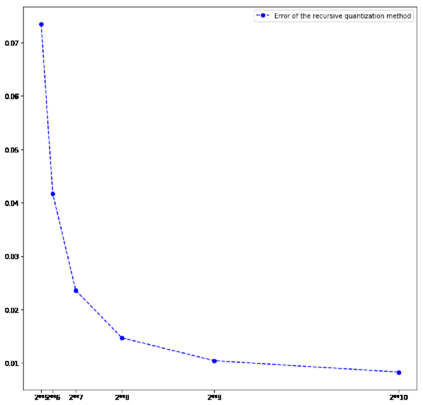
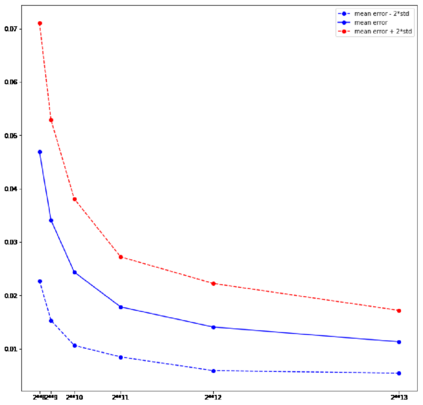
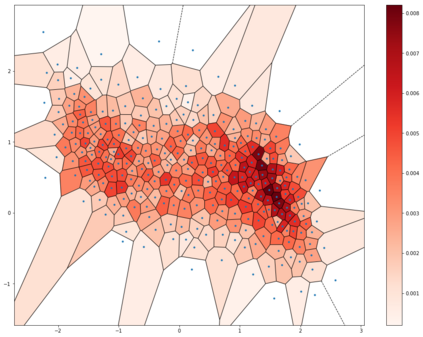
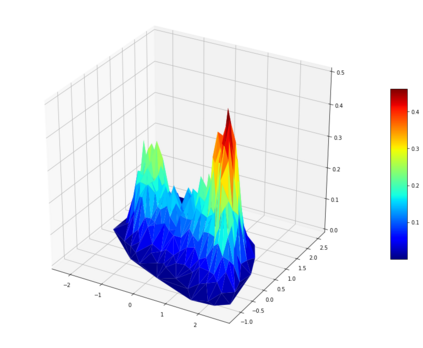
In this paper, we study three numerical schemes for the McKean-Vlasov equation \[\begin{cases} \;dX_t=b(t, X_t, \mu_t) \, dt+\sigma(t, X_t, \mu_t) \, dB_t,\: \\ \;\forall\, t\in[0,T],\;\mu_t \text{ is the probability distribution of }X_t, \end{cases}\] where $X_0$ is a known random variable. Under the assumption on the Lipschitz continuity of the coefficients $b$ and $\sigma$, our first result proves the convergence rate of the particle method with respect to the Wasserstein distance, which extends a previous work [BT97] established in one-dimensional setting. In the second part, we present and analyse two quantization-based schemes, including the recursive quantization scheme (deterministic scheme) in the Vlasov setting, and the hybrid particle-quantization scheme (random scheme, inspired by the $K$-means clustering). Two examples are simulated at the end of this paper: Burger's equation and the network of FitzHugh-Nagumo neurons in dimension 3.
翻译:在本文中,我们研究了McKan-Vlasov等式的三种数字方案 \ [\ begin{cases}\;dX_t=b(t, X_t,\mu_t)\, d\\sgma(t, X_t,\mu_t)\, dB_t;\\\\\\\\\\\Forall\, t\in[0,T]\;\mu_t\ text{是X_t,\end{cases}的概率分布,其中$X_t=0是一个已知的随机变量。在利普西茨系数的连续性假设 $b$和$\sgmas的假设下,我们的第一个结果证明了粒子方法与瓦瑟斯坦距离的趋同率,它延续了先前在一维萨洛夫设置的工程[BT97], t;在第二部分,我们介绍和分析两个基于裁量性的方案, 包括Vlasov 的递解分解方案(deministicn) 方案。在Vlasov 3 的平质阵积-qol-cal-qumal-chal-cal-cal-cal-cumation sumetal-cal-chal-cal-chalumational-chal-chmissional-cald imalpalpalpalpalpalpald imalpalpalpalpalmal-pal-pald smalmalmald 方案是3.