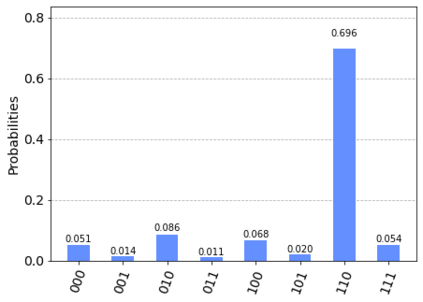
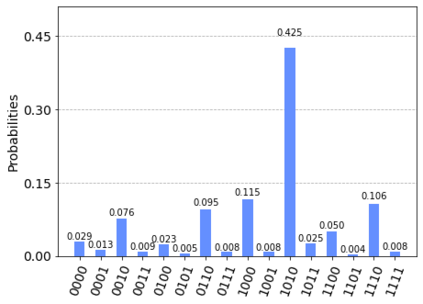
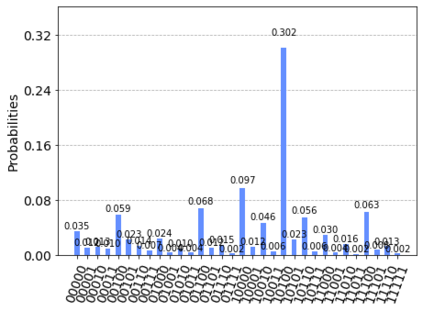
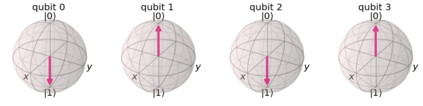
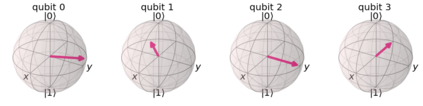
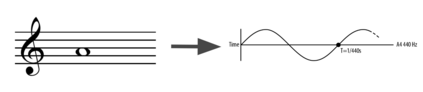
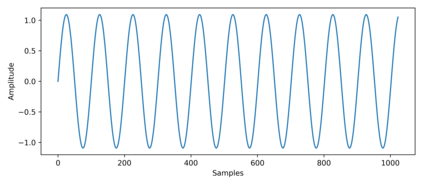
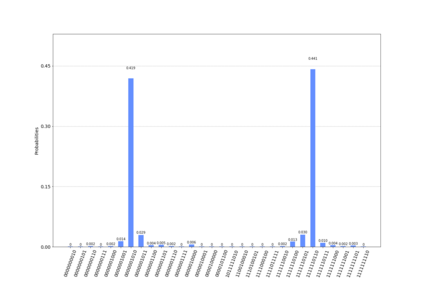
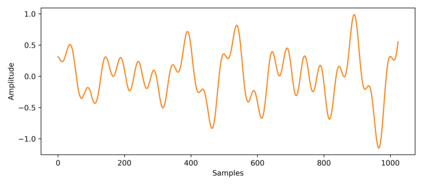
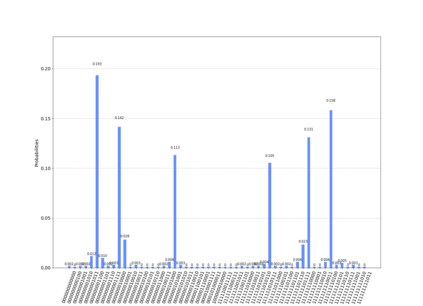
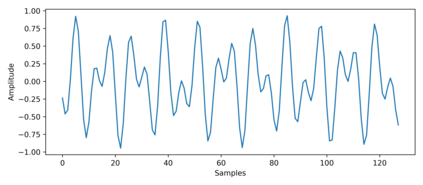
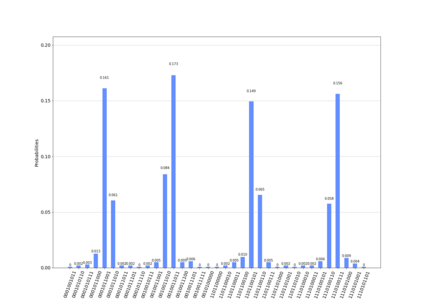
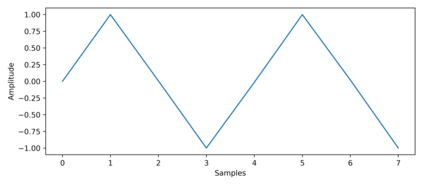
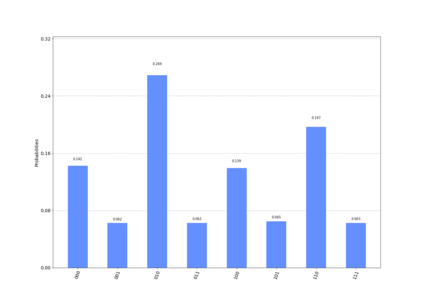
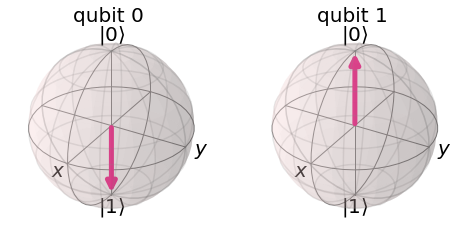
In quantum information processing (QIP), the quantum Fourier transform (QFT) has a plethora of applications [1] [2] [3]: Shor's algorithm and phase estimation are just a few well-known examples. Shor's quantum factorization algorithm, one of the most widely quoted quantum algorithms [4] [5] [6] relies heavily on the QFT and efficiently finds integer prime factors of large numbers on quantum computers [4]. This seminal ground-breaking design for quantum algorithms has triggered a cascade of viable alternatives to previously unsolvable problems on a classical computer that are potentially superior and can run in polynomial time. In this work we examine the QFT's structure and implementation for the creation of a quantum music note detection algorithm both on a simulated and a real quantum computer. Though formal approaches [7] [1] [8] [9] exist for the verification of quantum algorithms, in this study we limit ourselves to a simpler, symbolic representation which we validate using the symbolic SymPy [10] [11] package which symbolically replicates quantum computing processes. The algorithm is then implemented as a quantum circuit, using IBM's qiskit [12] library and finally period detection is exemplified on an actual single musical tone using a varying number of qubits.
翻译:在量量信息处理(QIP)中,量信息变量量量量的量 Fourier 变异(QFT)有很多应用[[[2][3][3]]:Shor的算法和阶段估计只是几个众所周知的例子。Shor的量子因子化算算算法,这是最广泛引用的量子算算法之一[4][5][6],严重依赖QFT,并且高效率地在量子计算机[4]中找到大量数字的整数的整数质质子质子质变变(QFT),在数量信息处理(QIP)中,量子变变量量量量(QFT)的算法有很多[[2][3][3][6] 。这种量子算法的原始破碎设计引发了一系列一系列可行的替代方法,取代了古典计算机上无法解决的问题,而古典计算机可能优于多音时可以运行。在这项工作中,我们审查QFT的结构和实施QF的结构,以在模拟和真正的量计算期间,用IBM'sqskit's missuals lax ex aminal