Games and Computational Complexity

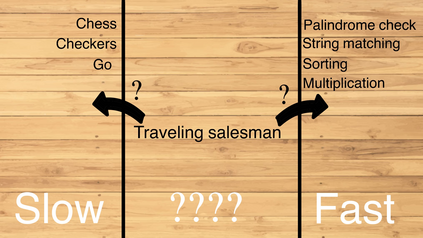
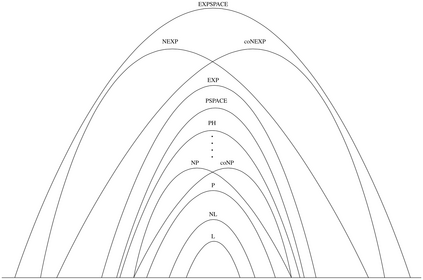
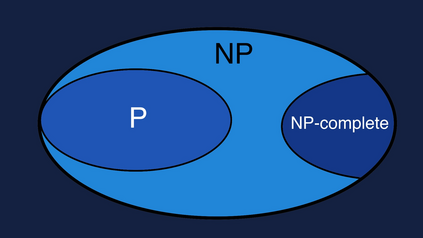
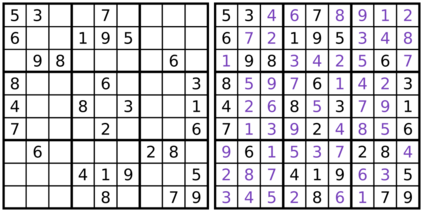
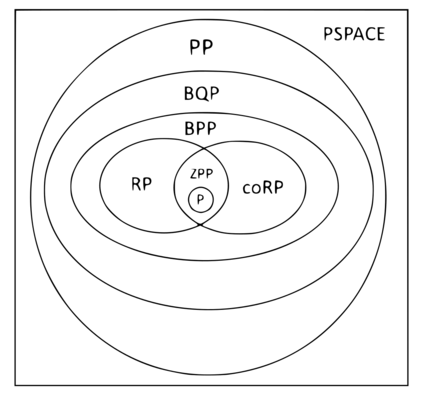
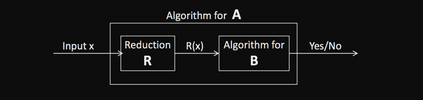
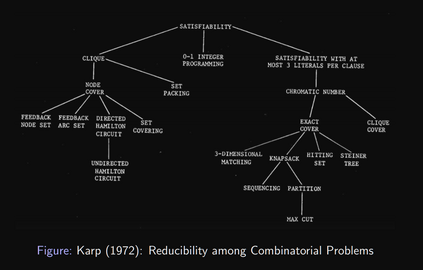
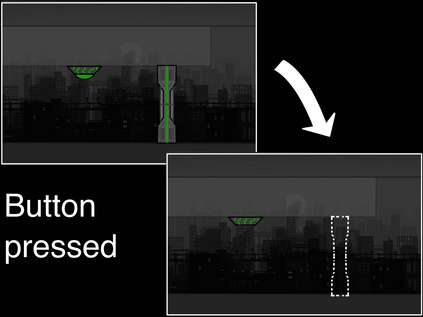
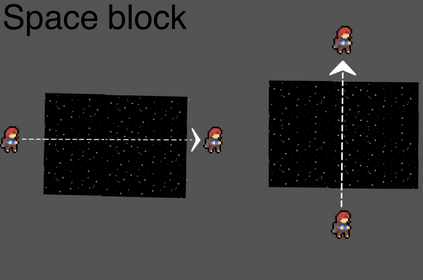
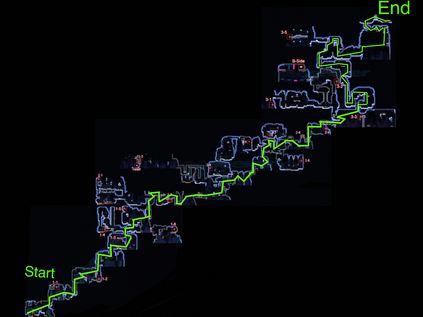
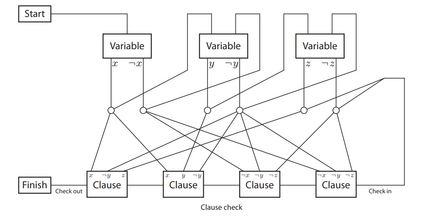
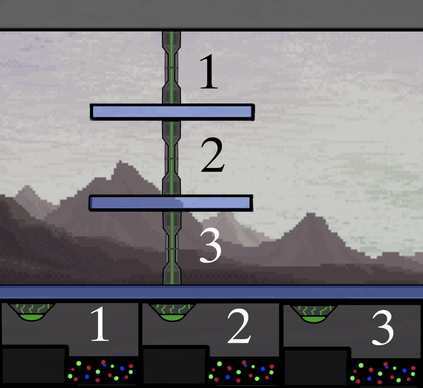
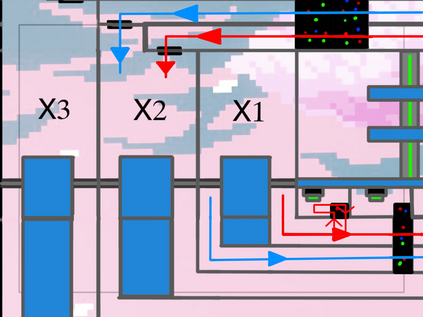
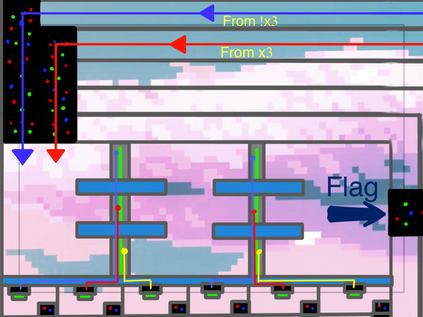
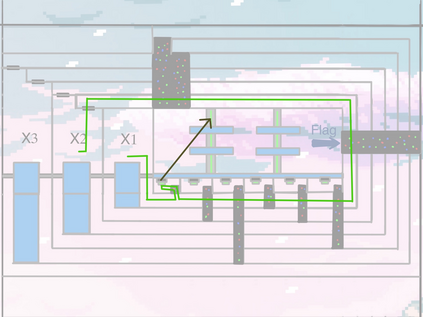
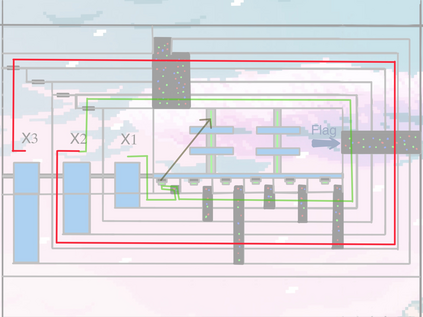
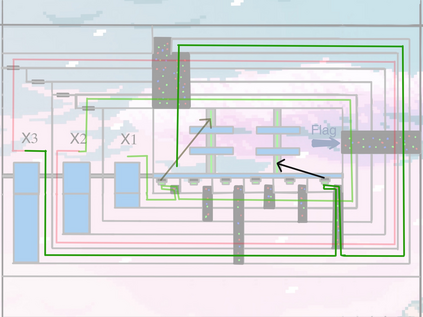
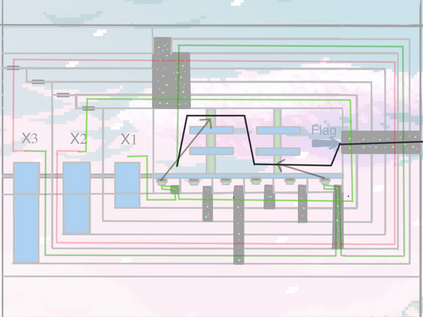
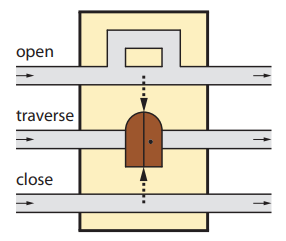
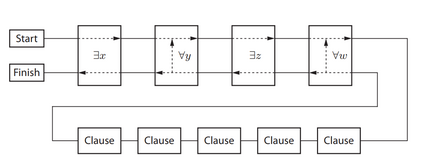
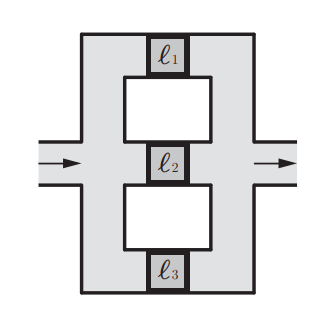
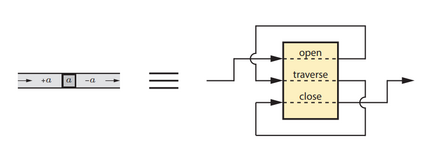
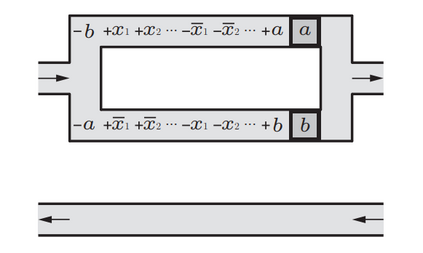
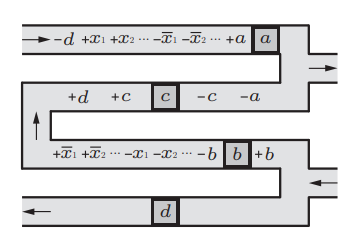
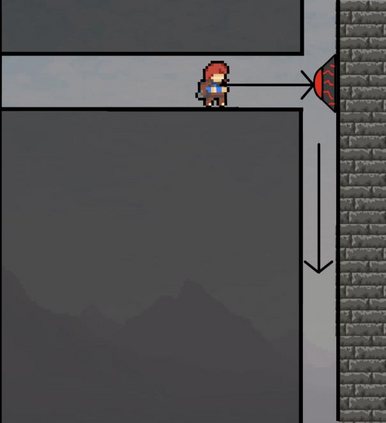
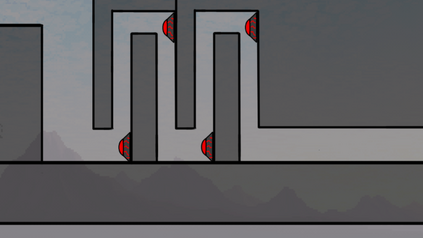
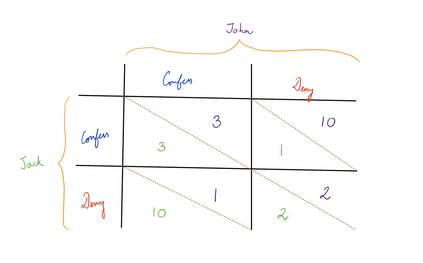
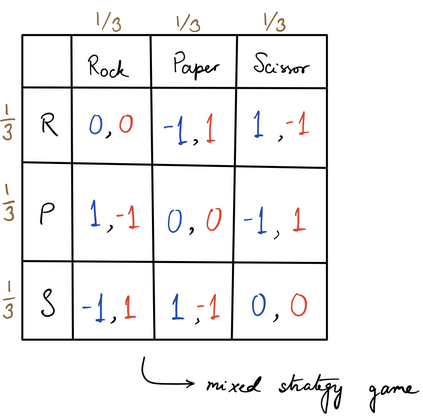
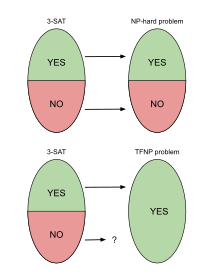
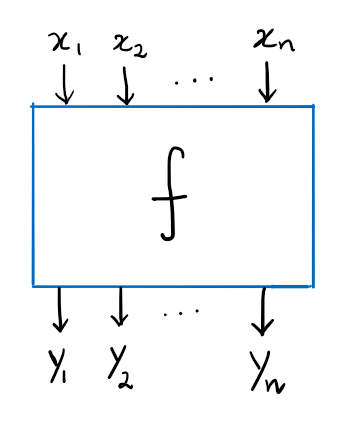
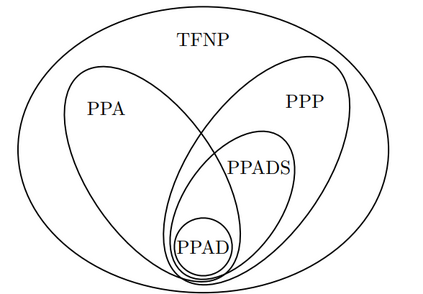
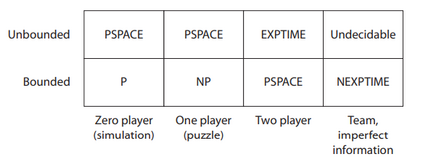
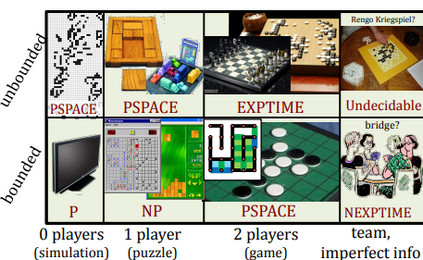
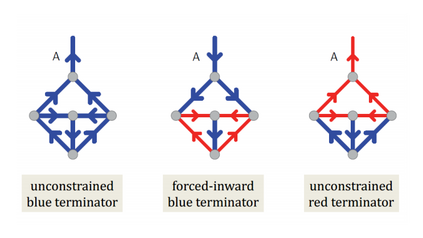
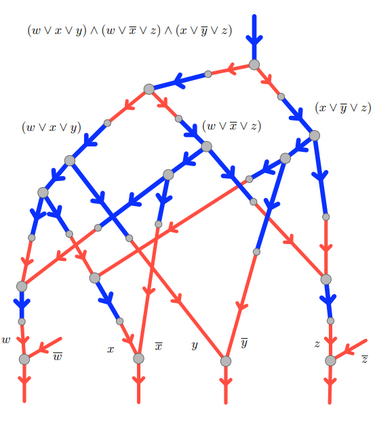
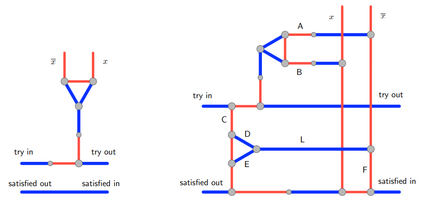
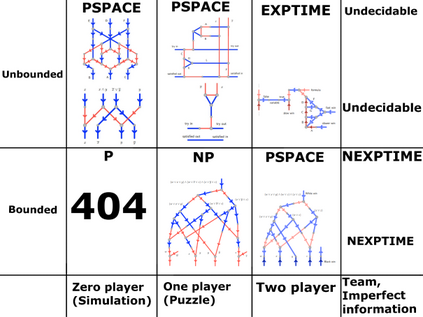
Computers are known to solve a wide spectrum of problems, however not all problems are computationally solvable. Further, the solvable problems themselves vary on the amount of computational resources they require for being solved. The rigorous analysis of problems and assigning them to complexity classes what makes up the immense field of complexity theory. Do protein folding and sudoku have something in common? It might not seem so but complexity theory tells us that if we had an algorithm that could solve sudoku efficiently then we could adapt it to predict for protein folding. This same property is held by classic platformer games such as Super Mario Bros, which was proven to be NP-complete by Erik Demaine et. al. This article attempts to review the analysis of classical platformer games. Here, we explore the field of complexity theory through a broad survey of literature and then use it to prove that that solving a generalized level in the game "Celeste" is NP-complete. Later, we also show how a small change in it makes the game presumably harder to compute. Various abstractions and formalisms related to modelling of games in general (namely game theory and constraint logic) and 2D platformer video games, including the generalized meta-theorems originally formulated by Giovanni Viglietta are also presented.