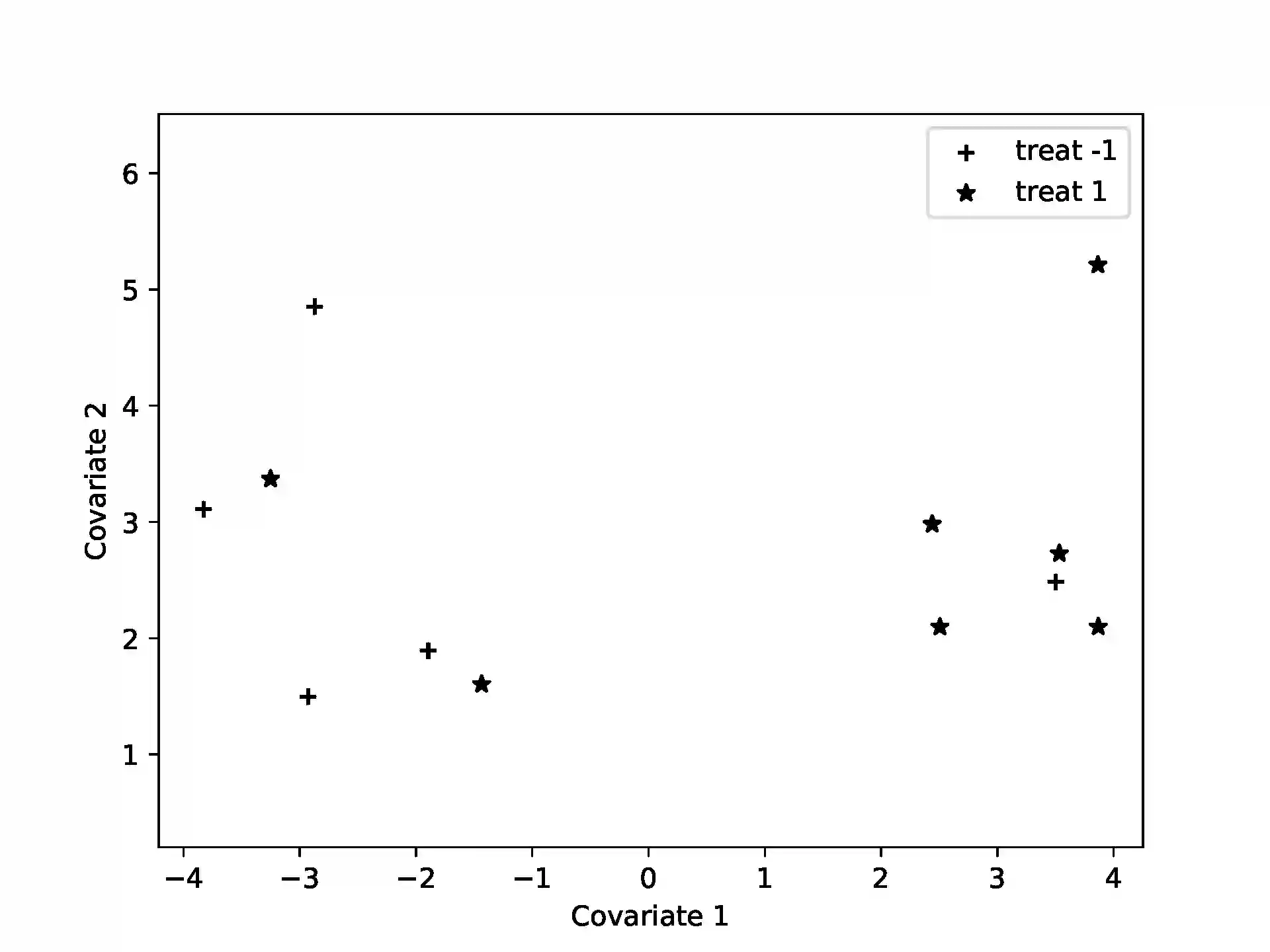
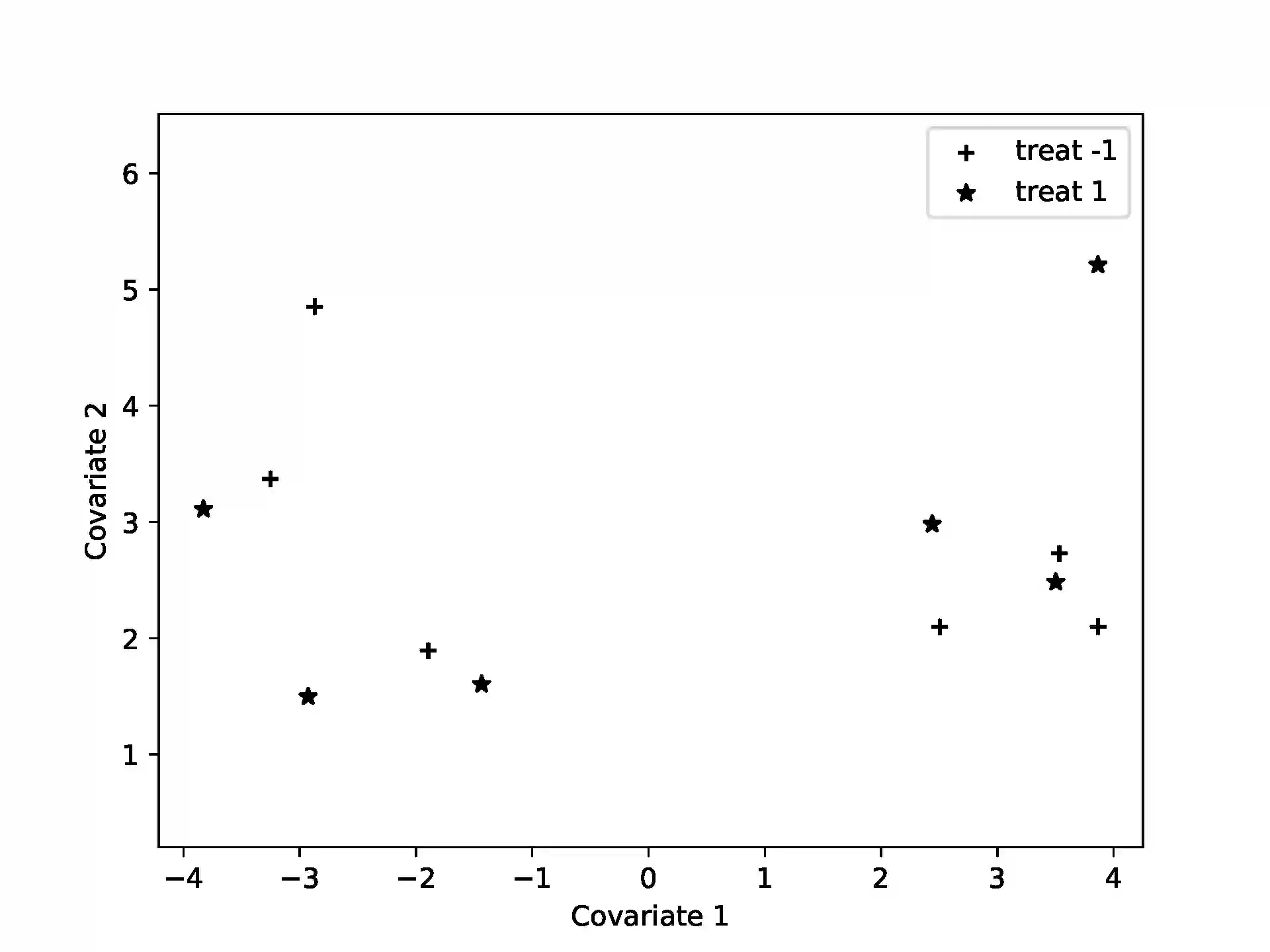
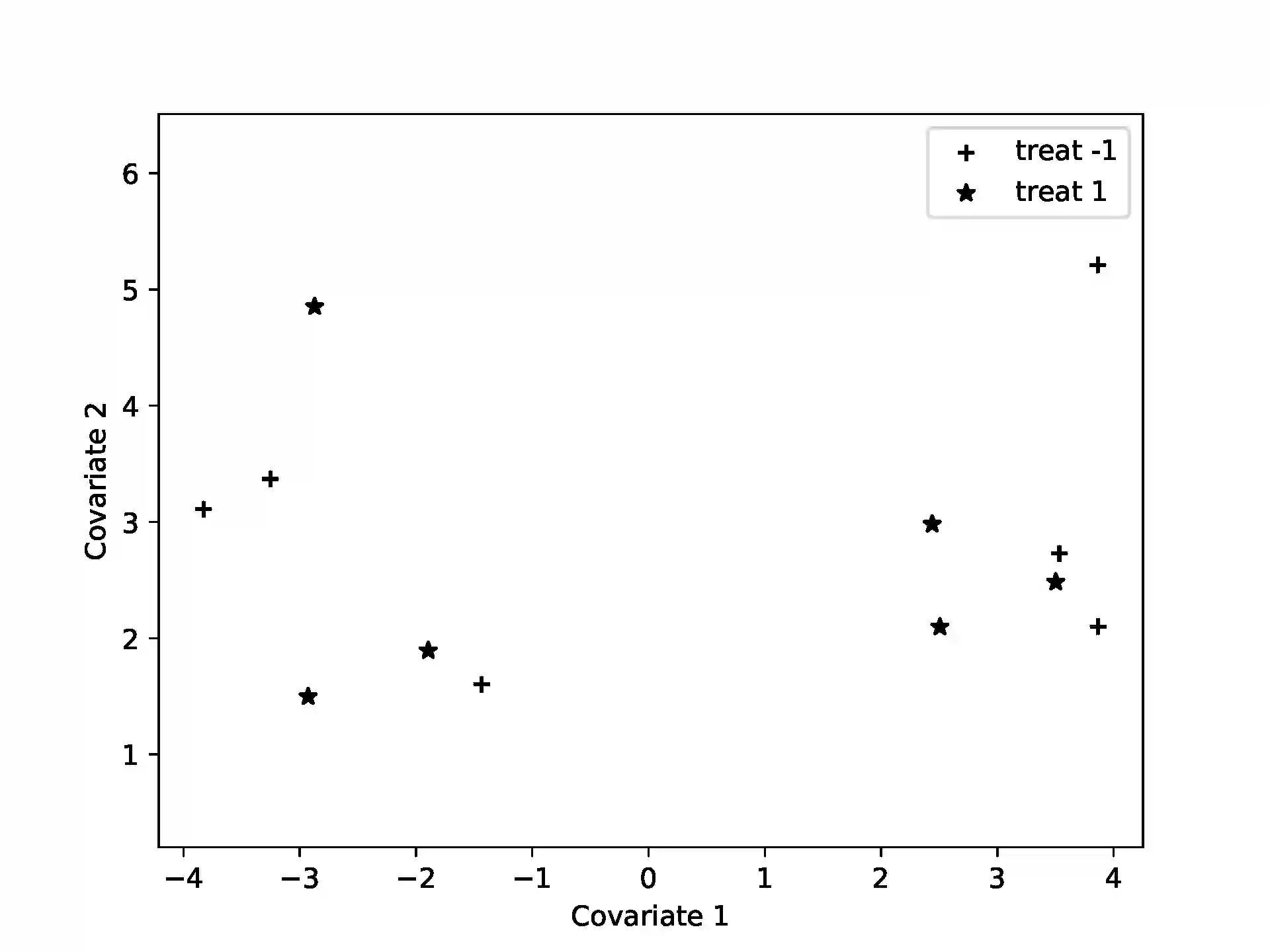
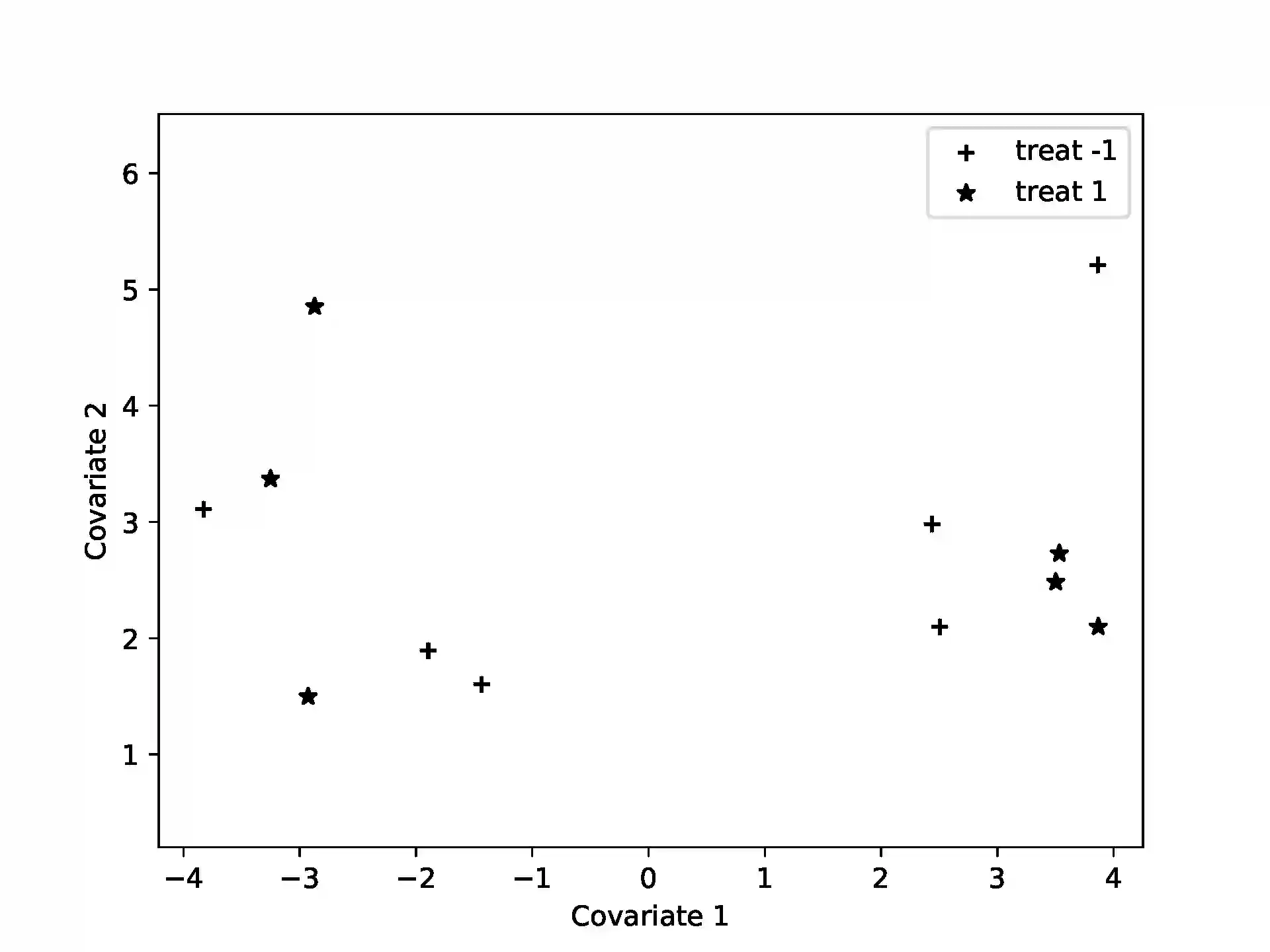
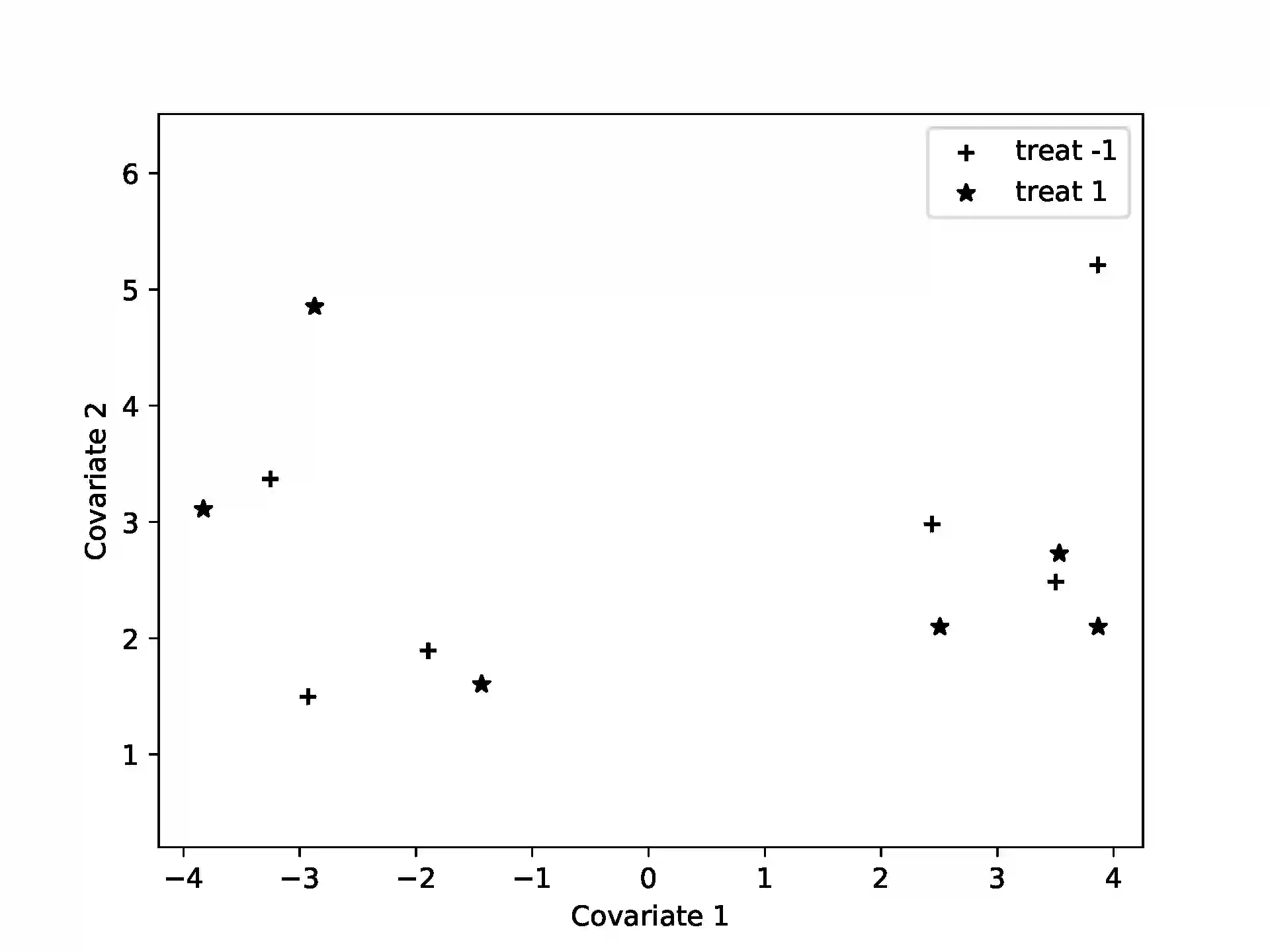
Algorithmic discrepancy theory seeks efficient algorithms to find those two-colorings of a set that minimize a given measure of coloring imbalance in the set, its {\it discrepancy}. The {\it Euclidean discrepancy} problem and the problem of balancing covariates in randomized trials have efficient randomized algorithms based on the Gram-Schmidt walk (GSW). We frame these problems as quantum Ising models, for which variational quantum algorithms (VQA) are particularly useful. Simulating an example of covariate-balancing on an IBM quantum simulator, we find that the variational quantum eigensolver (VQE) and the quantum approximate optimization algorithm (QAOA) yield results comparable to the GSW algorithm.
翻译:算法差异理论寻求高效的算法,以找到能够最大限度地减少一组中色不平衡的两种颜色,即其 ~it 差异} 。 ~Euclidean 差异} 问题和随机试验中平衡共差的问题基于Gram-Schmidt 步行( GSW) 的高效随机算法。 我们将这些问题描述为量子Ising 模型, 其变量算法(VQA)特别有用 。 模拟IBM 量子模拟器的共变平衡示例, 我们发现变量量量单和量子优化算法(QAOA)产生与GSW 算法相似的结果。