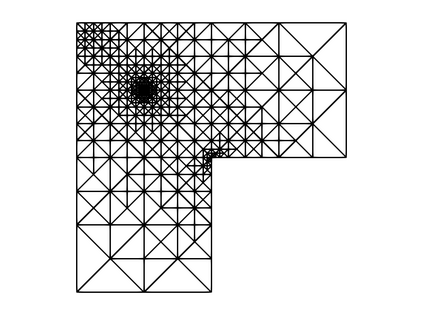
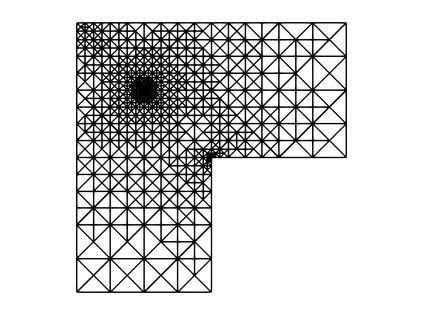
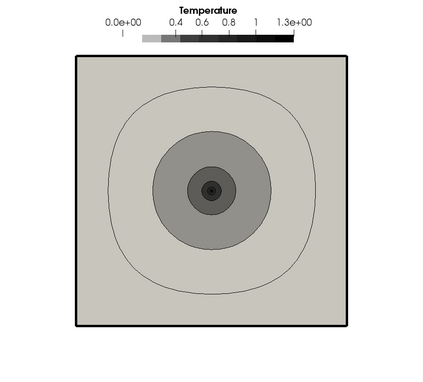
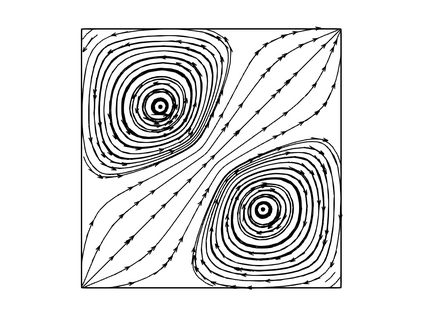
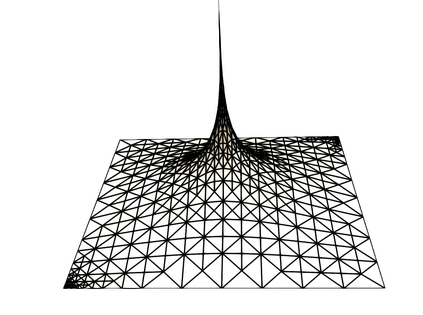
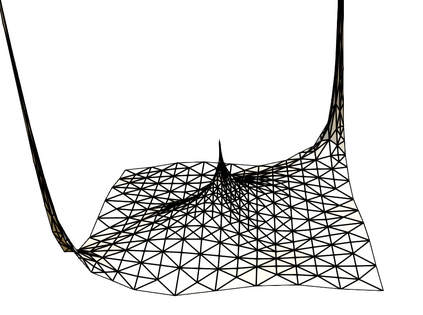
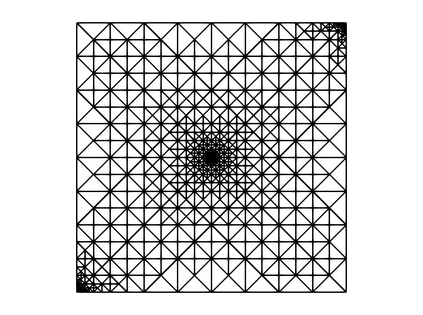
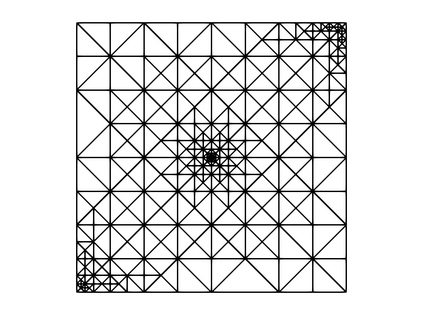
In Lipschitz domains, we study a Darcy-Forchheimer problem coupled with a singular heat equation by a nonlinear forcing term depending on the temperature. By singular we mean that the heat source corresponds to a Dirac measure. We establish the existence of solutions for a model that allows a diffusion coefficient in the heat equation depending on the temperature. For such a model, we also propose a finite element discretization scheme and provide an a priori convergence analysis. In the case that the aforementioned diffusion coefficient is constant, we devise an a posteriori error estimator and investigate reliability and efficiency properties. We conclude by devising an adaptive loop based on the proposed error estimator and presenting numerical experiments.
翻译:在Lipschitz 域中,我们研究达西-福什海默问题,同时根据温度,用非线性强制术语来研究单热方程式。单数是指热源与Dirac测量值相对应。我们为允许根据温度在热方程式中设定扩散系数的模型确定解决方案。对于这样一个模型,我们还提出一个有限元素离散方案,并提供先验的趋同分析。如果上述扩散系数是恒定的,我们设计一个后遗误测算器,并调查可靠性和效率特性。我们最后根据拟议的误测计和数字实验设计一个适应循环。