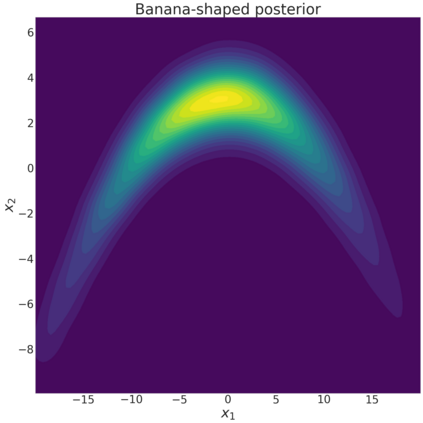
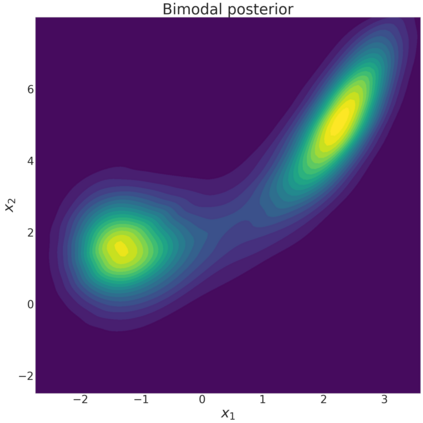
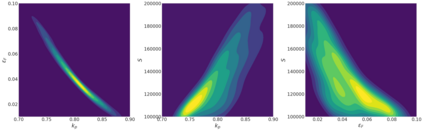
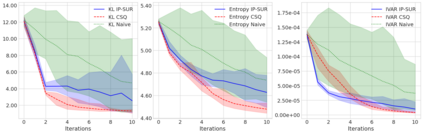
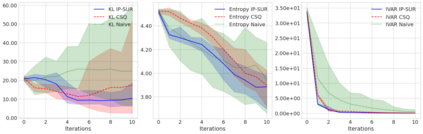
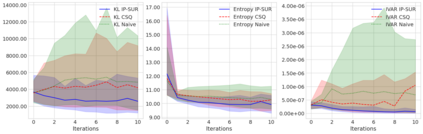
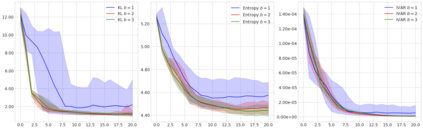
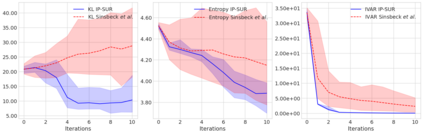
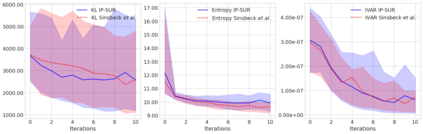
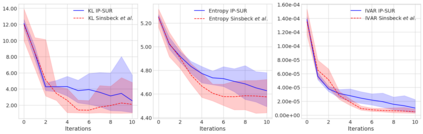
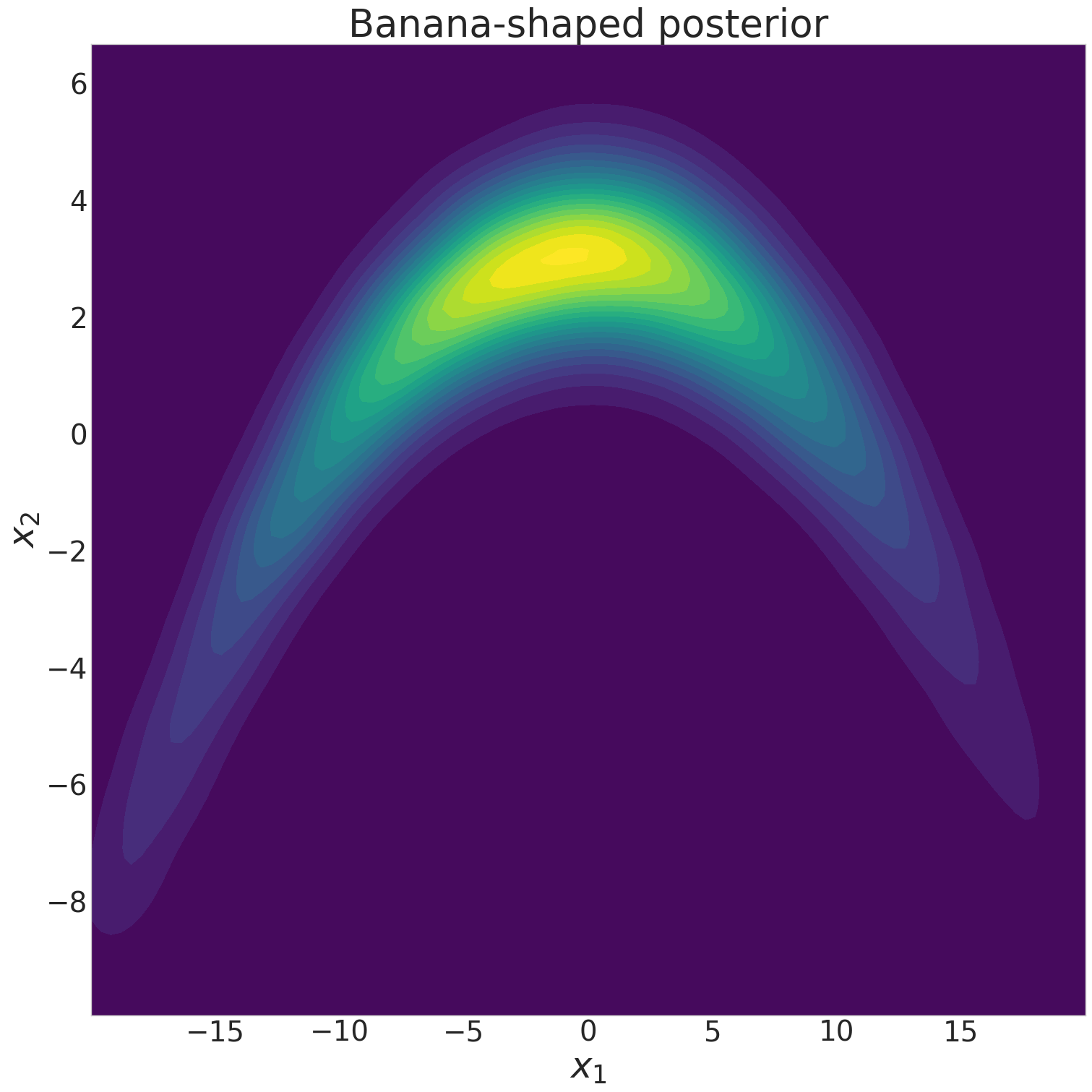
Sequential design is a highly active field of research in active learning which provides a general framework for the design of computer experiments to make the most of a low computational budget. It has been widely used to generate efficient surrogate models able to replace complex computer codes, most notably for uncertainty quantification, Bayesian optimization, reliability analysis or model calibration tasks. In this work, a sequential design strategy is developed for Bayesian inverse problems, in which a Gaussian process surrogate model serves as an emulator for a costly computer code. The proposed strategy is based on a goal-oriented I-optimal criterion adapted to the Stepwise Uncertainty Reduction (SUR) paradigm. In SUR strategies, a new design point is chosen by minimizing the expectation of an uncertainty metric with respect to the yet unknown new data point. These methods have attracted increasing interest as they provide an accessible framework for the sequential design of experiments while including almost-sure convergence for the most-widely used metrics. In this paper, a weighted integrated mean square prediction error is introduced and serves as a metric of uncertainty for the newly proposed IP-SUR (Inverse Problem Stepwise Uncertainty Reduction) sequential design strategy derived from SUR methods. This strategy is shown to be tractable for both scalar and multi-output Gaussian process surrogate models with continuous sample paths, and comes with theoretical guarantee for the almost-sure convergence of the metric of uncertainty. The premises of this work are highlighted on various test cases in which the newly derived strategy is compared to other naive and sequential designs (D-optimal designs, Bayes risk minimization).
翻译:暂无翻译