Finding Minimum Connected Subgraphs with Ontology Exploration on Large RDF Data

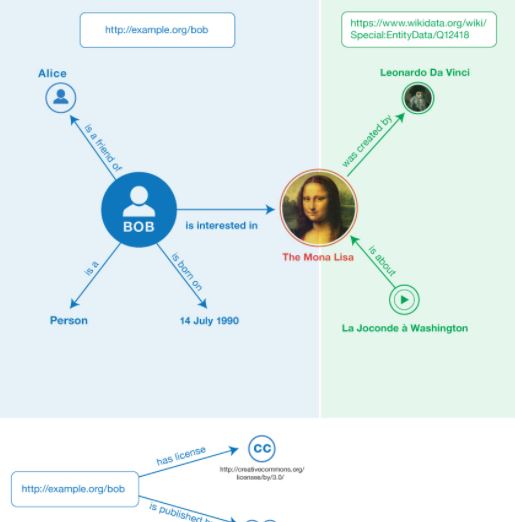
In this paper, we study the following problem: given a knowledge graph (KG) and a set of input vertices (representing concepts or entities) and edge labels, we aim to find the smallest connected subgraphs containing all of the inputs. This problem plays a key role in KG-based search engines and natural language question answering systems, and it is a natural extension of the Steiner tree problem, which is known to be NP-hard. We present RECON, a system for finding approximate answers. RECON aims at achieving high accuracy with instantaneous response (i.e., sub-second/millisecond delay) over KGs with hundreds of millions edges without resorting to expensive computational resources. Furthermore, when no answer exists due to disconnection between concepts and entities, RECON refines the input to a semantically similar one based on the ontology, and attempt to find answers with respect to the refined input. We conduct a comprehensive experimental evaluation of RECON. In particular we compare it with five existing approaches for finding approximate Steiner trees. Our experiments on four large real and synthetic KGs show that RECON significantly outperforms its competitors and incurs a much smaller memory footprint.