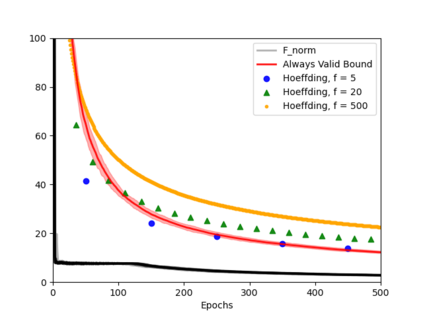
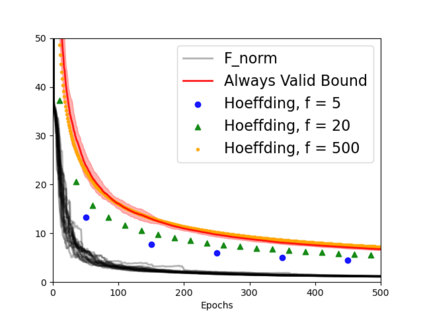
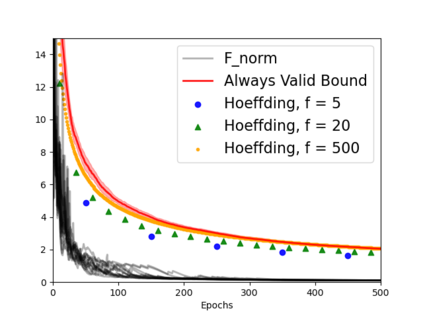
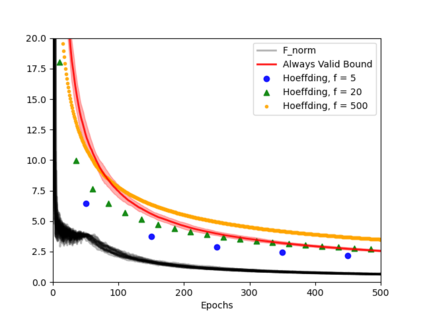
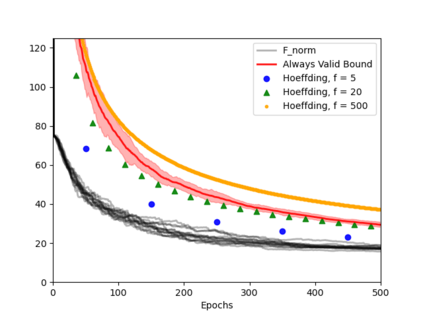
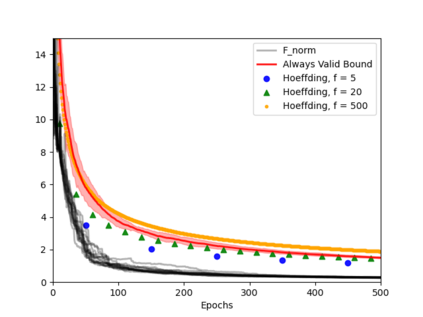
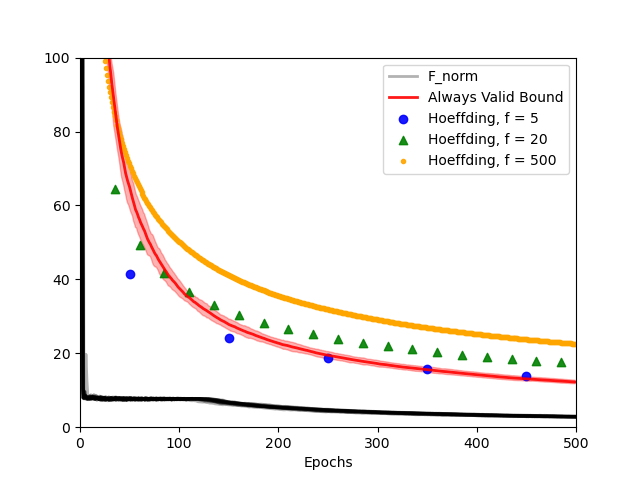
Always-valid concentration inequalities are increasingly used as performance measures for online statistical learning, notably in the learning of generative models and supervised learning. Such inequality advances the online learning algorithms design by allowing random, adaptively chosen sample sizes instead of a fixed pre-specified size in offline statistical learning. However, establishing such an always-valid type result for the task of matrix completion is challenging and far from understood in the literature. Due to the importance of such type of result, this work establishes and devises the always-valid risk bound process for online matrix completion problems. Such theoretical advances are made possible by a novel combination of non-asymptotic martingale concentration and regularized low-rank matrix regression. Our result enables a more sample-efficient online algorithm design and serves as a foundation to evaluate online experiment policies on the task of online matrix completion.
翻译:长期有效的集中不平等日益被用作在线统计学习的业绩计量,特别是在学习基因模型和受监督的学习方面;这种不平等通过允许随机、适应性选择的抽样规模,而不是离线统计学习的固定特定规模,从而推进在线学习算法的设计;然而,为完成矩阵的任务确定这种总有效的类型结果具有挑战性,而且远非文献所理解。由于这类结果的重要性,这项工作为在线矩阵的完成问题建立和设计了始终有效的风险约束程序。这种理论进步是非简易马丁格尔集中和正规化低级矩阵回归的新组合所促成的。我们的结果使得能够进行更具有样本效率的在线算法设计,并成为评价在线矩阵完成任务的在线实验政策的基础。