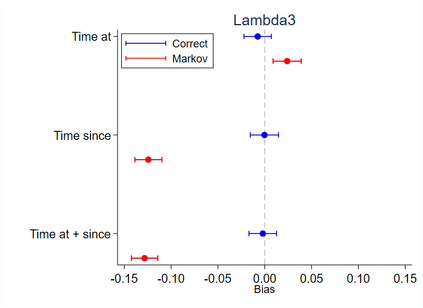
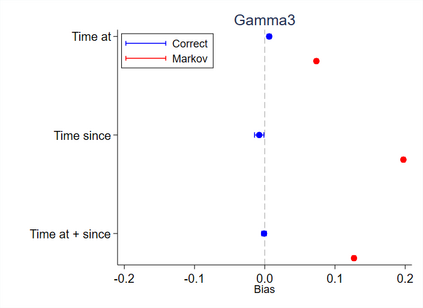
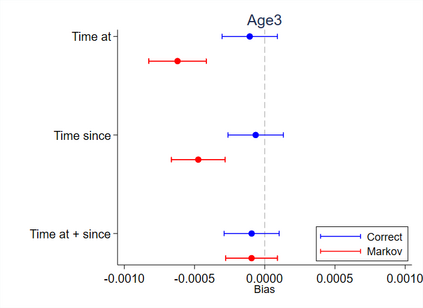
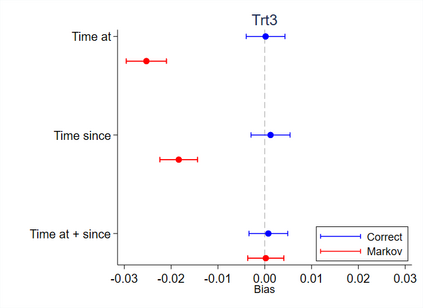
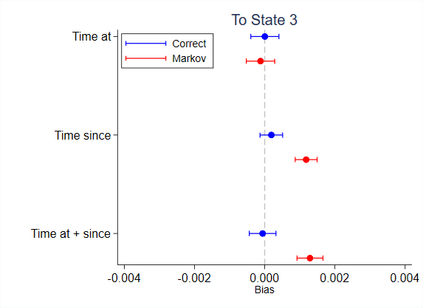
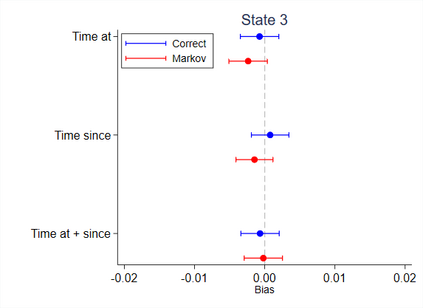
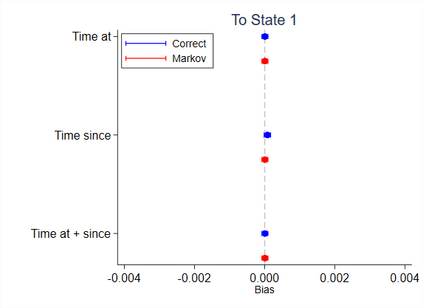
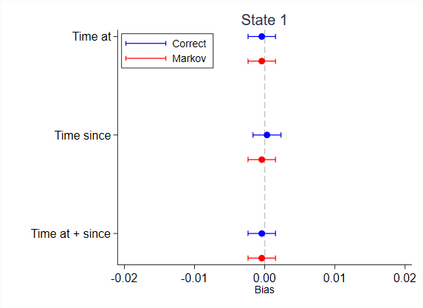
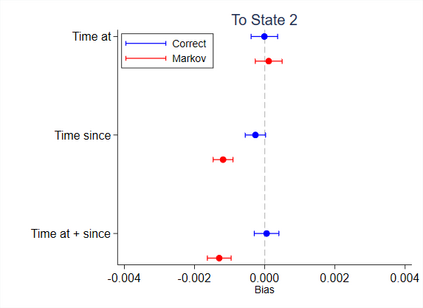
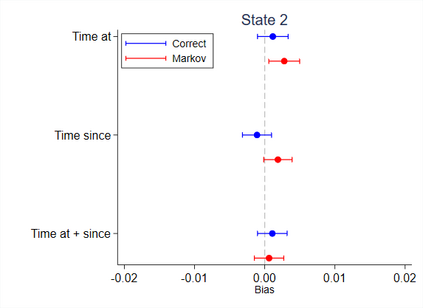
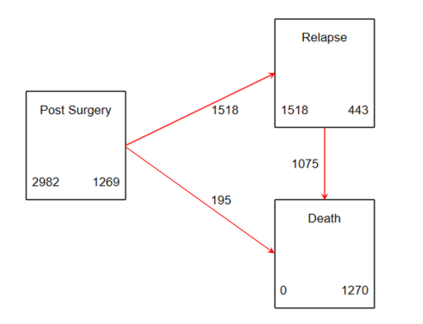
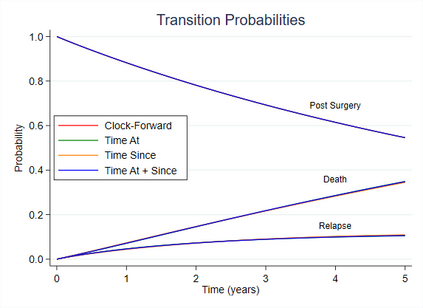
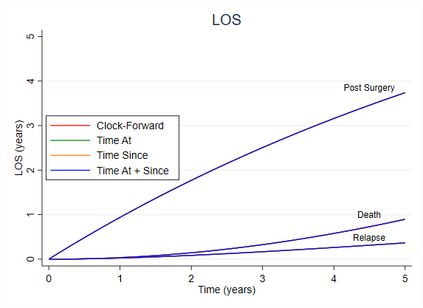
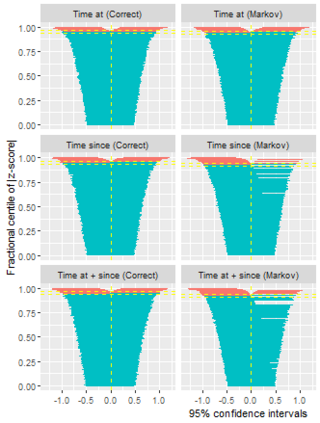
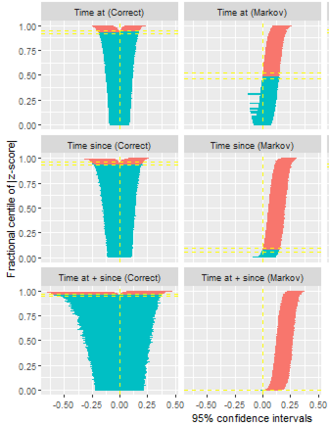
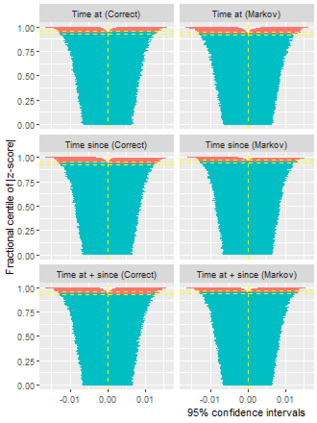
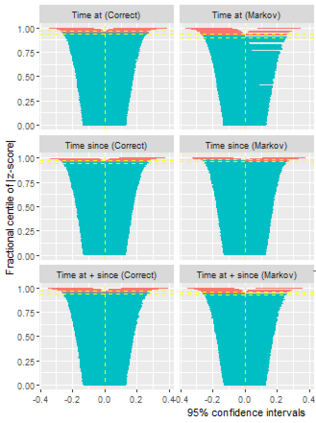
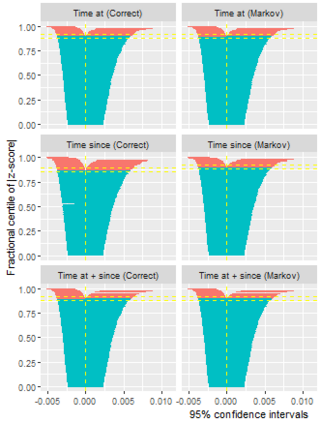
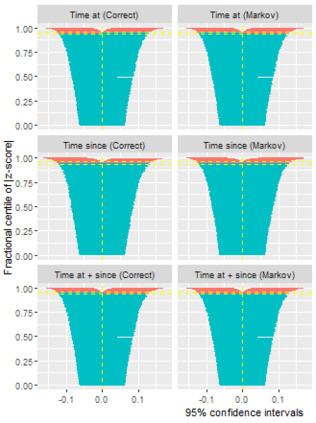
Multi-state survival analysis considers several potential events of interest along a disease pathway. Such analyses are crucial to model complex patient trajectories and are increasingly being used in epidemiological and health economic settings. Multi-state models often make the Markov assumption, whereby an individual's future trajectory is dependent only upon their present state, not their past. In reality, there may be transitional dependence upon either previous events and/or more than one timescale, for example time since entry to the current or previous state(s). The aim of this study was to develop an illness-death Weibull model allowing for multiple timescales to impact the future risk of death. Following this, we evaluated the performance of the multiple timescale model against a Markov illness-death model in a set of plausible simulation scenarios when the Markov assumption was violated. Guided by a study in breast cancer, data were simulated from Weibull baseline distributions, with hazard functions dependent on single and multiple timescales. Markov and non-Markov models were fitted to account for/ignore the underlying data structure. Ignoring the presence of multiple timescales led to bias in underlying transition rates between states and associated covariate effects, while transition probabilities and lengths of stay were fairly robustly estimated. Further work may be needed to evaluate different estimands or more complex multi-state models. Software implementations in Stata are also described for simulating and estimating multiple timescale multi-state models.
翻译:多 St国生存分析考虑到疾病路径上的若干潜在关注事件。这种分析对于模拟复杂的病人轨迹至关重要,并且越来越多地用于流行病学和健康经济环境。多州模型往往作出Markov假设,即个人未来轨迹仅取决于其当前状态,而不是过去。在现实中,可能过渡依赖以往事件和/或超过一个时间尺度,例如自进入当前或以往状态以来的一段时间,可能过渡依赖以往事件和/或超过一个时间尺度,例如从进入当前或以往状态以来的一段时间。本研究的目的是开发一个疾病死亡Wibbull模型,允许多个时标数影响未来死亡风险。此后,我们用一套可信的模拟假设假设假设,即个人未来轨迹仅取决于其当前状态,而不是过去。在乳腺癌研究的指导下,对韦布尔基线分布的数据进行模拟,其危害功能取决于单一和多个时间尺度。Markov 和非马尔科夫模型被安装到基本数据结构的核算/标识。在多时间尺度上描述多个时标数模式的存在,导致在马科夫假设的过渡期间出现偏差,同时估算各国之间的平稳过渡和稳定。