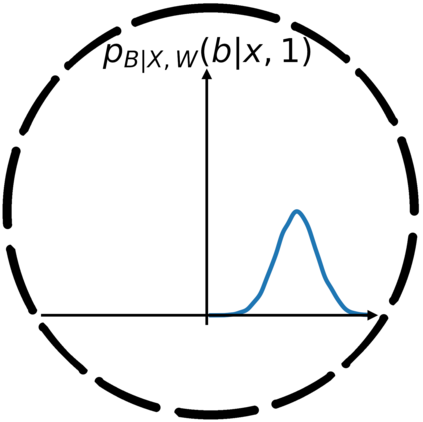
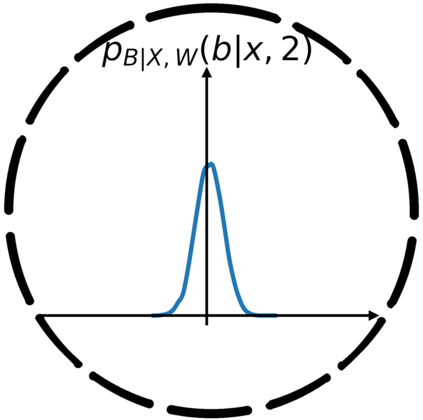
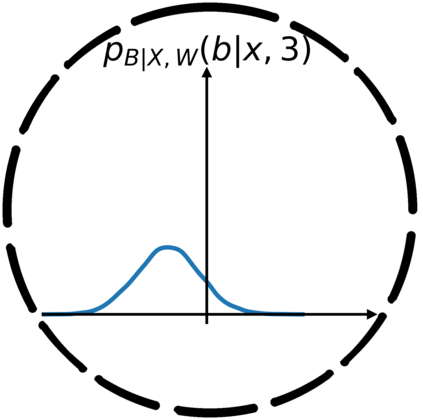
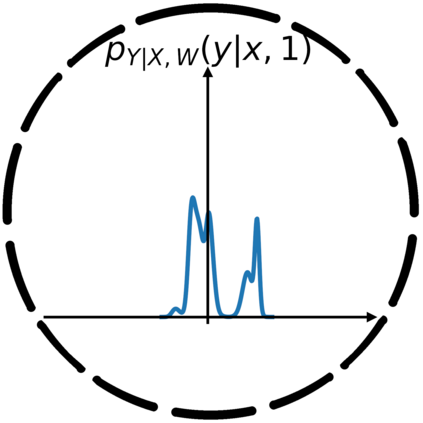
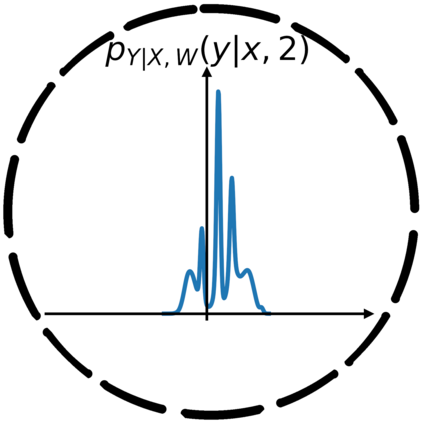
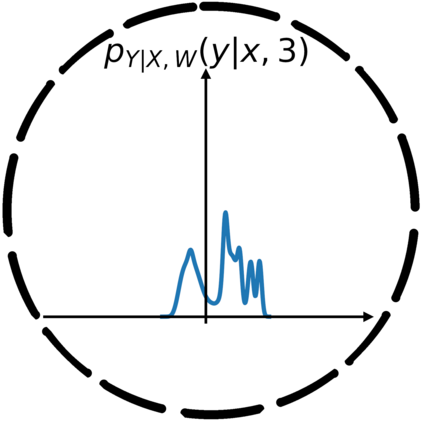
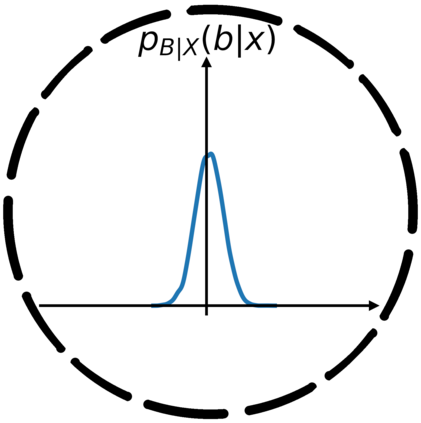
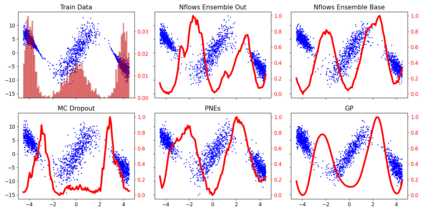
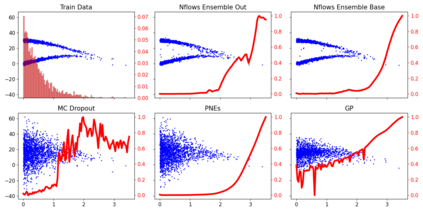
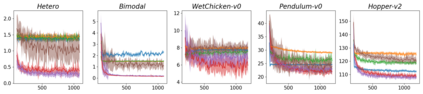
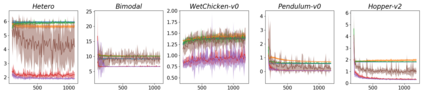
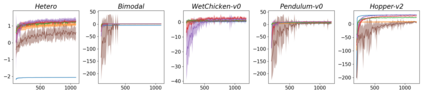
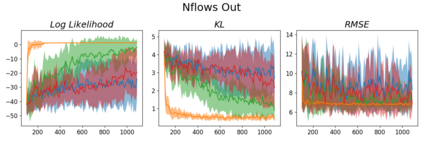
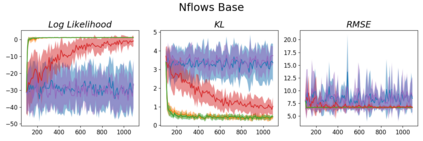
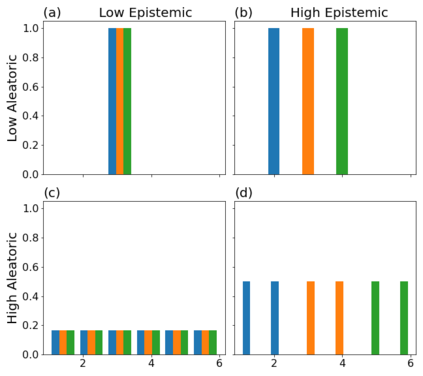
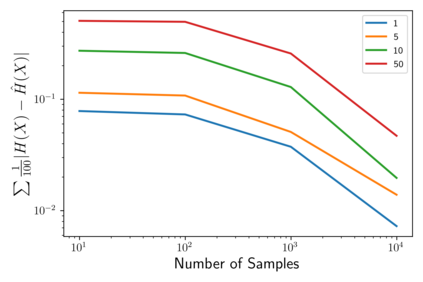
In this work, we demonstrate how to reliably estimate epistemic uncertainty while maintaining the flexibility needed to capture complicated aleatoric distributions. To this end, we propose an ensemble of Normalizing Flows (NF), which are state-of-the-art in modeling aleatoric uncertainty. The ensembles are created via sets of fixed dropout masks, making them less expensive than creating separate NF models. We demonstrate how to leverage the unique structure of NFs, base distributions, to estimate aleatoric uncertainty without relying on samples, provide a comprehensive set of baselines, and derive unbiased estimates for differential entropy. The methods were applied to a variety of experiments, commonly used to benchmark aleatoric and epistemic uncertainty estimation: 1D sinusoidal data, 2D windy grid-world ($\it{Wet Chicken}$), $\it{Pendulum}$, and $\it{Hopper}$. In these experiments, we setup an active learning framework and evaluate each model's capability at measuring aleatoric and epistemic uncertainty. The results show the advantages of using NF ensembles in capturing complicated aleatoric while maintaining accurate epistemic uncertainty estimates.
翻译:在这项工作中,我们展示了如何可靠地估计适应性不确定性,同时保持必要的灵活性以捕捉复杂的大气分布。 为此,我们提出一个常态流动(NF)的组合,这是模拟大气不确定性的最先进的模型。 集合是通过一套固定的排泄面罩建立的,比另外的NF模型的费用要低一些。 我们演示了如何利用NF的独特结构、基分布,在不依赖样本的情况下估计疏松性不确定性,提供一套全面的基线,并对不同的昆虫得出不偏的估计数。 这种方法被应用于各种实验,通常用来作为测算耐受体和感性不确定性估计的基准:1D类类类的类流数据,2D型风网格-世界($\it{Wet chicken}), $\it{Pendulum}$, 和$\it{Hopper}$。 在这些实验中,我们设置了一个积极的学习框架,并评价每个模型测量耐受体和癫痫不确定性的能力。 研究结果显示,同时利用复杂型号数据库的优势。